关联矩阵是用结点与支路的关系描述有向图的拓扑性质。
回路矩阵是用回路与支路的关系描述有向图的拓扑性质。
割集矩阵是用割集与支路的关系描述有向图的拓扑性质。
本节仅介绍关联矩阵以及用它表示的基尔霍夫定律的矩阵形式。
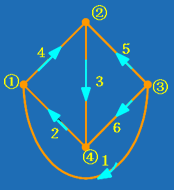
一条支路连接某两个结点,则称该支路与这两个结点相关联。支路与结点的关联性质可以用关联矩阵描述。设有向图的结点数为 n ,支路数为 b ,且所有结点与支路均加以编号。于是,该有向图的关联矩阵为一个
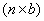 阶的矩阵,用
阶的矩阵,用 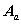 表示。它的每一行对应一个结点,每一列对应一条支路,它的任一元素
表示。它的每一行对应一个结点,每一列对应一条支路,它的任一元素 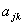 定义如下:
定义如下: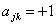 ,表示支路 k 与结点 j 关联并且它的方向背离结点;
,表示支路 k 与结点 j 关联并且它的方向背离结点; 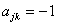 ,表示支路 k 与结点 j 关联并且它指向结点 ,表示支路 k 与结点 j 关联并且它指向结点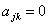 ,表示支路 k 与结点 j 无关联。 ,表示支路 k 与结点 j 无关联。 对于图 1 所示的有向图,它的关联矩阵是 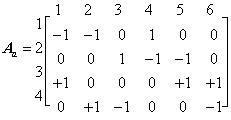 |
 |
关联矩阵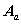 的特点: 的特点: |
图 1 |
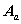 的每一列元素之和为零。
的每一列元素之和为零。② 矩阵中任一行可以从其他 n-1 行中导出,即只有 n-1 行是独立的。
如果把
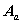 的任一行划去,剩下的
的任一行划去,剩下的  矩阵用
矩阵用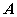 表示,并称为降阶关联矩阵(今后主要用这种降阶关联矩阵,所以往往略去“降阶”二字),被划去的行对应的结点可以当作参考结点。
表示,并称为降阶关联矩阵(今后主要用这种降阶关联矩阵,所以往往略去“降阶”二字),被划去的行对应的结点可以当作参考结点。例如,若以结点 4 为参考结点,把上式中
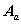 的第 4 行划去,得
的第 4 行划去,得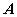
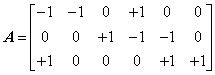
若以结点 3 为参考结点,把上式中
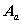 的第 3 行划去,得
的第 3 行划去,得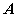
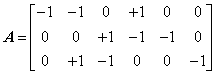
矩阵
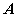 的某些列将只具有一个 +1 或一个-1,每一个这样的列必对应于与参考结点相关联的一条支路。
的某些列将只具有一个 +1 或一个-1,每一个这样的列必对应于与参考结点相关联的一条支路。注意:给定
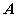 可以确定
可以确定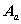 ,从而画出有向图。
,从而画出有向图。
