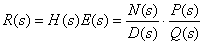
式中
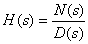 ,
,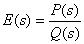 ,而
,而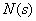 、
、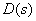 、
、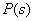 、
、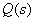 都是 s 的多项式。用部分分式法求响应的原函数时,
都是 s 的多项式。用部分分式法求响应的原函数时,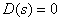 和
和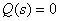 的根。
的根。令分母D(s)=0,解出根pi,( i=1,…, n ),
同时,令分母Q(s)=0,解出根 pj,(j=1,…, m ) 。那么,
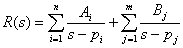
则响应的时域形式为:
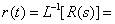
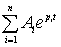 +
+ 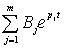
其中响应
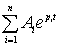 中包含
中包含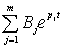 中包含
中包含 的根(即网络函数的极点),属于强制分量。因此,自由分量是由网络函数决定的,强制分量是由强制电源决定的。
的根(即网络函数的极点),属于强制分量。因此,自由分量是由网络函数决定的,强制分量是由强制电源决定的。可见,D(s)=0 的根对决定R(s)的变化规律起决定性的作用。由于单位冲激响应h(t) 的特性就是时域响应中自由分量的特性,所以分析网络函数的极点与冲激响应的关系就可预见时域响应的特点。若网络函数为真分式且分母具有单根,则网络的冲激响应为:
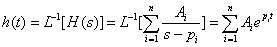
上式说明:
1)若
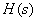 的极点
的极点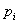 都位于负实轴上,为负实根时,
都位于负实轴上,为负实根时,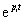 为衰减指数函数,则
为衰减指数函数,则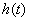 将随t 的增大而衰减,称这种电路是稳定的;若有一个极点
将随t 的增大而衰减,称这种电路是稳定的;若有一个极点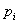 为正实根时,
为正实根时,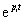 为增长的指数函数,则
为增长的指数函数,则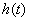 将随t 的增长而增长;而且
将随t 的增长而增长;而且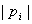 越大,衰减或增长的速度越快,称这种电路是不稳定的。
越大,衰减或增长的速度越快,称这种电路是不稳定的。2)当极点
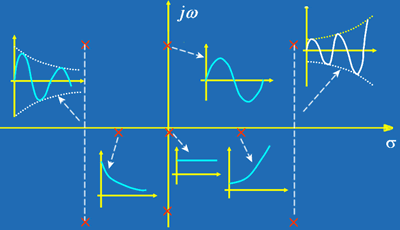
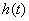 是以指数曲线为包络线的正弦函数,其实部的正或负确定增长或衰减的正弦项。
是以指数曲线为包络线的正弦函数,其实部的正或负确定增长或衰减的正弦项。3)当
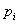 为虚根时,则将是纯正弦项。
为虚根时,则将是纯正弦项。
| 图中画出了网络函数的极点分别为负实数、正实数、虚数以及共轭复数时,对应的时域响应的波形。 注意: 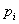 仅由网络的结构及元件值确定,因而将 仅由网络的结构及元件值确定,因而将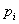 称为该网络变量的自然频率或固有频率。 称为该网络变量的自然频率或固有频率。
|