对于某个固定的,H(jω)通常为一个复数,可表示为
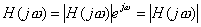 /
/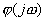
式中,
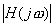 为网络函数在频率 ω 处的模值,
为网络函数在频率 ω 处的模值,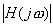 随频率 ω 变化的关系为幅度频率响应,简称幅频特性;
随频率 ω 变化的关系为幅度频率响应,简称幅频特性;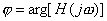 随频率 ω 变化的关系为相位频率响应,简称相频特性。由于:
随频率 ω 变化的关系为相位频率响应,简称相频特性。由于: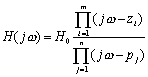
所以幅频特性为:
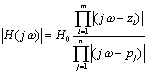
相频特性为:
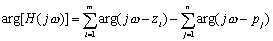
若已知网络函数的极点和零点,则按上式便可计算对应的频率响应,同时还可通过s 平面上零极点位置定性描绘出频率响应。
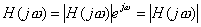 /
/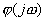
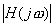 为网络函数在频率 ω 处的模值,
为网络函数在频率 ω 处的模值,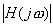 随频率 ω 变化的关系为幅度频率响应,简称幅频特性;
随频率 ω 变化的关系为幅度频率响应,简称幅频特性;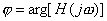 随频率 ω 变化的关系为相位频率响应,简称相频特性。由于:
随频率 ω 变化的关系为相位频率响应,简称相频特性。由于: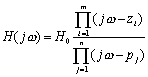
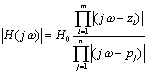
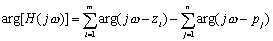
上一篇有向图的关联矩阵
下一篇网络函数的极点和零点