- 含有动态元件的电路称为动态电路。
动态电路所满足的电路方程称为输入输出方程。
基尔霍夫定律是分析电路的根本定律,适用于线性电路、非线性电路、时不变电路、时变电路。
对于一个简单的动态电路,已知电路元件参数 R、L、C,和电压源 us(t) ,求电容两端电压 uC (t) :
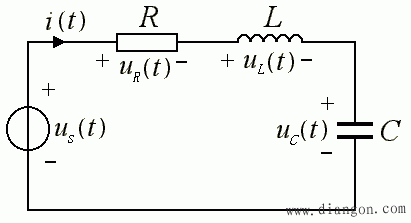
- 解决此问题的思路是:先写出 KVL 方程,然后利用电容、电感的电流电压约束关系代换未知量,最后将方程整理成只含一个要求的未知函数 uC (t) 的方程。
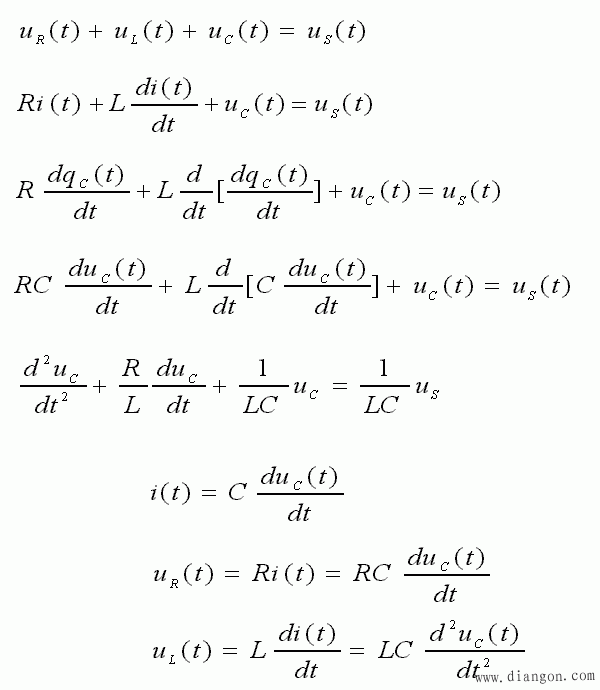
- 如上所示,只要求得 uC ( t ),就可求得 i、uR ( t )、uL ( t )。
对于一个较复杂的动态电路,已知电路元件参数R1、L1、C1、R2、L2、C2,和电压源 us( t ) ,求电流 i1 ( t ) 随时间的变化:
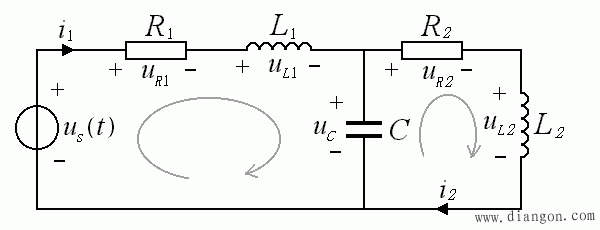
- 解决此问题的思路是:写出两个回路的 KVL 方程,利用电容、电感的电流电压约束关系代换未知量,并消去未知量 i2 ( t ),最后得到只含一个要求的未知函数 i1 ( t ) 的微分方程。
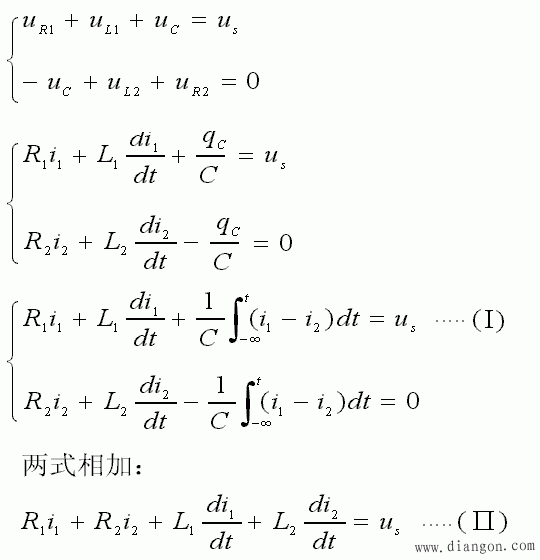
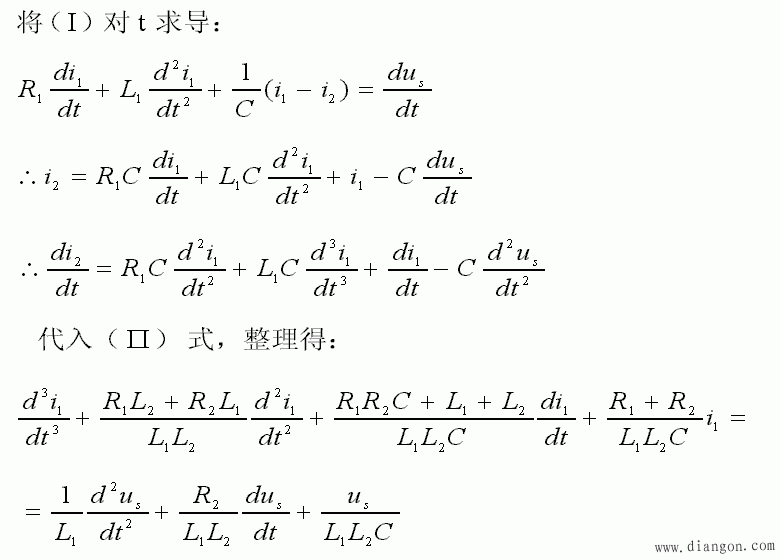
- 解出 i1 ( t ) 后,就可求得其它元件的电压和电流表达式了。
由以上分析可得结论:对于一般的动态电路,运用基尔霍夫定律,总可以得到一个单未知量的输入输出方程。电路越复杂,动态元件越多,得到的微分方程的阶数越高。
