一阶电路的零输入响应

动态电路在没有外加激励的条件下，仅靠电路中动态元件的初始储能而引起的电路响应，称为“零输入响应”。

1、RC 电路的零输入响应

图示电路，在 t < 0 ，开关一直打在 U 0 ，在 t ＝ 0 时刻，开关打向电阻 R ，即换路。问在 t > 0 ， u _C 、 u _R 、 i 如何变化？


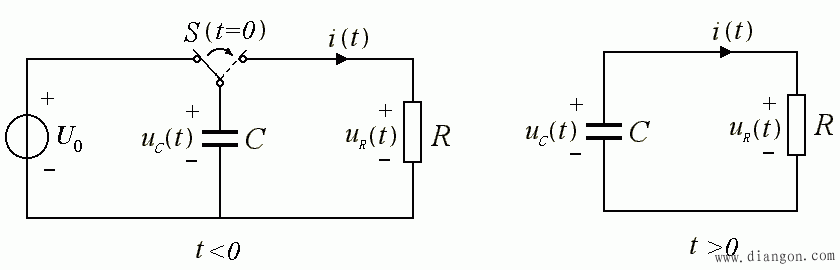
分析：

t < 0 时，u _C (t) ＝ U ₀ ；

t ＝ 0 时，在换路过程中，电容极板上没有电荷损失，u_C不变，即：

u _C ( 0₊ ) ＝ u _C ( 0_－ ) ＝ u _C ( 0 )

t > 0 ，即开关打向 R 后，电容 C 通过 R 放电，形成放电电流 i ，并在 R 上产生电压降 u_R ，随着 C 上电荷的减少， u_C 、u_R 、i 都在不断减小，直至为 0 。

只要求得 u C ，其它参量可通过下式求得：

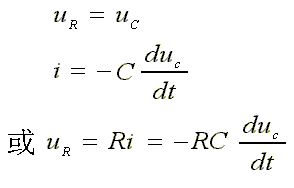
① 写出电路的输入输出方程：

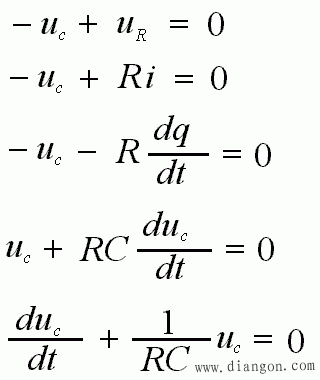
② 求解上述一阶线性齐次常系数微分方程：

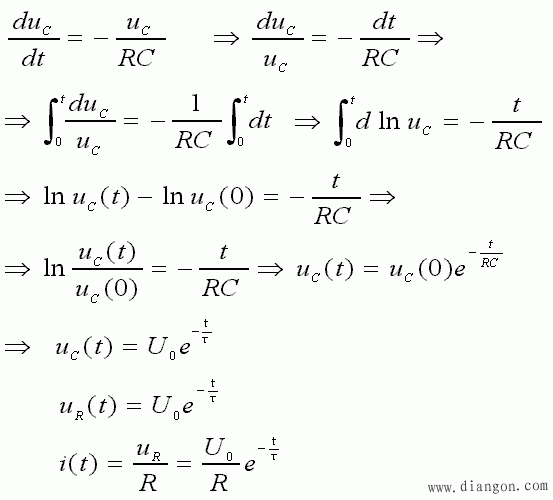
式中，τ＝RC，称为时间常数，放电常数。

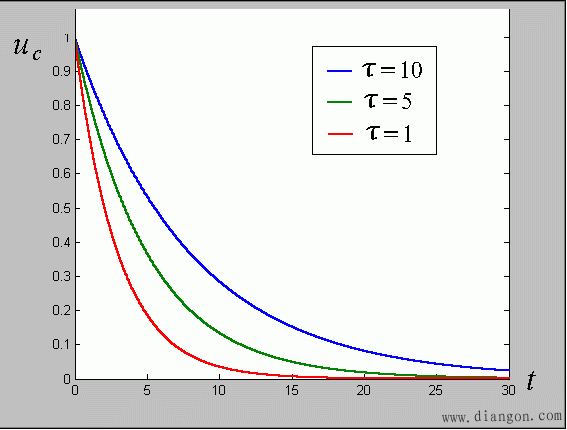
结论：电容放电随时间变化呈指数形式衰减。其衰减的快慢取决于时间常数τ＝RC。τ越大，衰减越慢，τ越小，衰减越快。

2、RL 电路的零输入响应

图示电路，在 t < 0 ，开关一直打在电流源 I₀ ，电感电流为 I₀。在 t ＝ 0 时刻，开关打向 R，即换路。问在 t > 0， u_L 、 u_R 、 i 随时间如何变化？


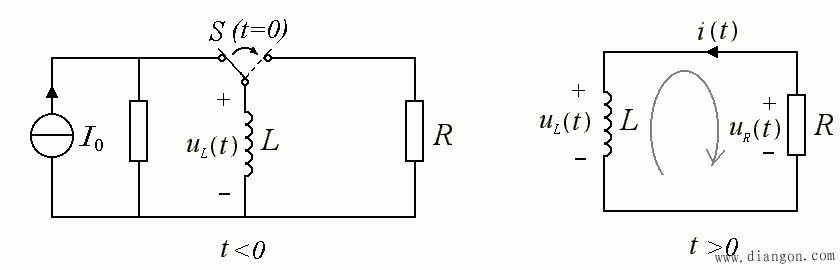
分析：

t < 0，L 中电流一直为 I₀ ；在 t ＝ 0 时刻换路，由于电压 u_L 有限 ( ＝0 ) ，i 不能跃变，故有：
i ( 0₊ ) ＝ i ( 0_－ ) ＝ i ( 0 ) ＝ I ₀

既然知道 i 的初始值，就以 i 为变量写出微分方程式。求得 i 后，可用下式求得其它电参量：


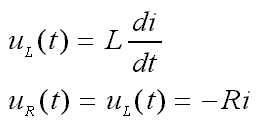
写出KVL方程，并求解：


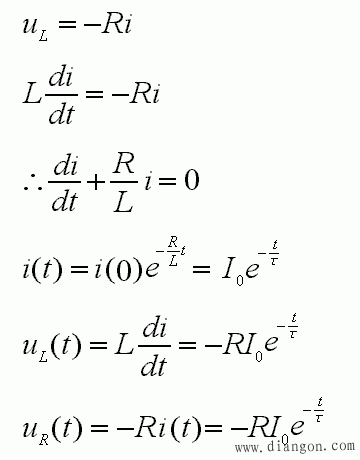
式中，τ＝L/R 为RL电路时间常数。


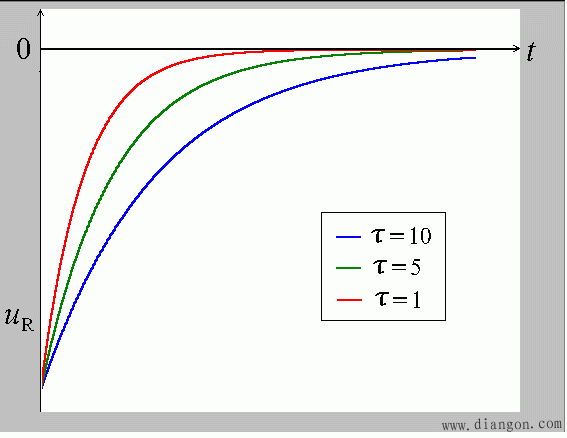
结论：电感中由初始储能引起的电流响应随时间变化呈指数形式衰减。其衰减的快慢取决于时间常数τ＝L/R。τ越大，衰减越慢，τ越小，衰减越快。u_L 与标定方向相反，其随时间变化也呈指数形式衰减。在此情况下，起电压源作用。