一阶电路的全响应

完全响应是指动态元件的初始储能不为零，同时输入也不为零的电路响应。

1、完全响应的分析方法

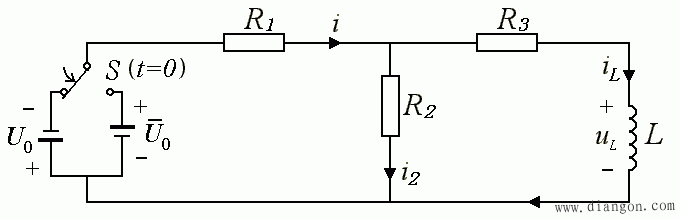
图示电路，换路前，开关打在左边 U ₀ 一方已很长时间。t＝0 时，开关打向右边电源。求 i，i_L 随时间的变化。

分两步：先求初始值，再计算 t≥ 0 时， i，i_L。

① 计算初始值 i ( 0₊ )、i_L( 0₊ )

在 t＝0_－ 以前，电路处于稳态，L 相当于短路，根据此时的等效电路，可计算出支路电流的初始值：

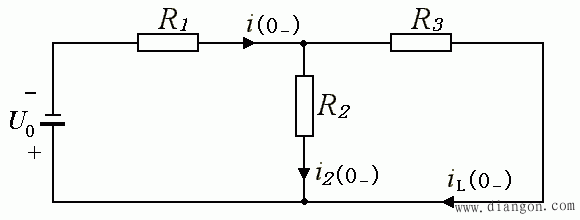
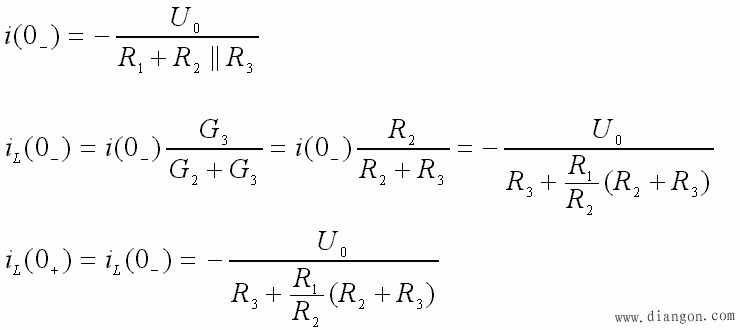
在 t = 0₊ 时刻，L 相当于一个大小为 i_L ( 0₊ ) 的电流源。根据此时刻的等效电路，可计算得：

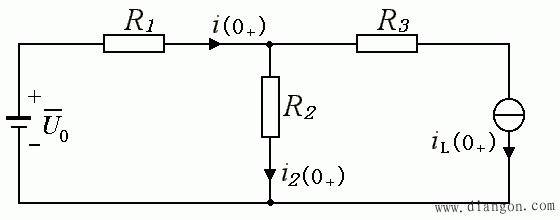
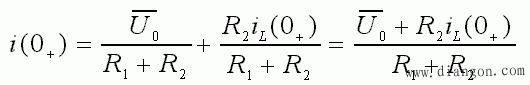
② 计算 t > 0 时 i ( t )、i_L( t )

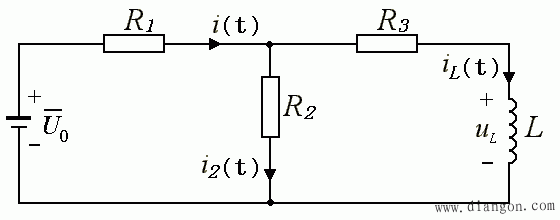
根据此时的等效电路，写出如下方程：

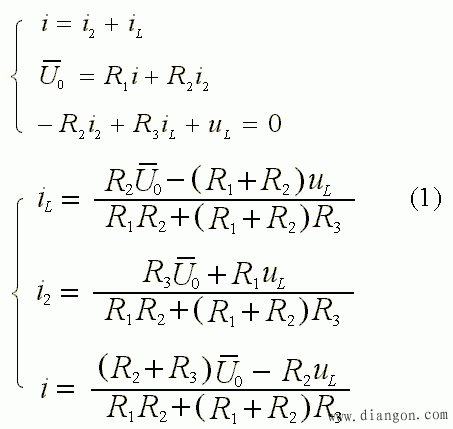
用 Ldi_L / dt 代换掉 (1) 中的 u _L， 再求解：

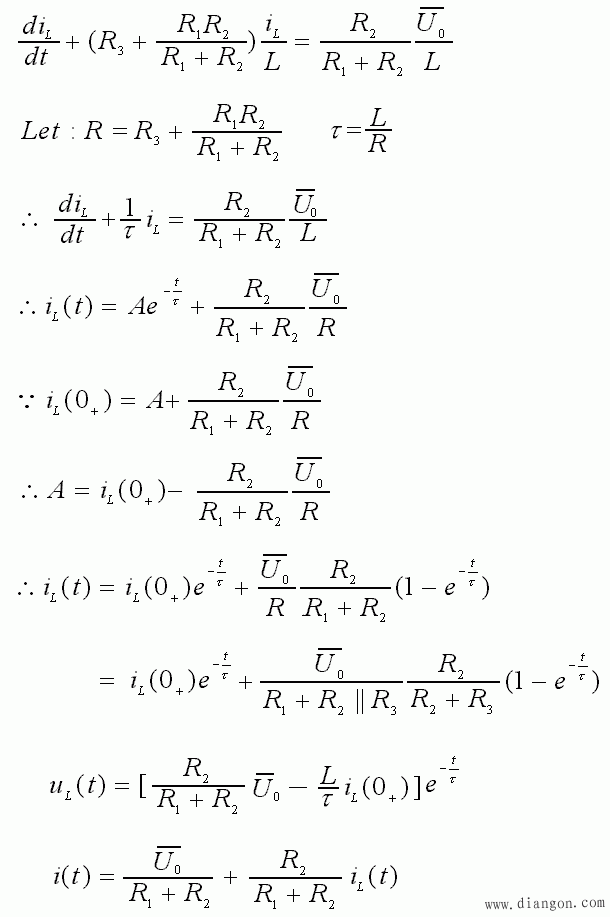
2、结果讨论

① 时间常数 τ

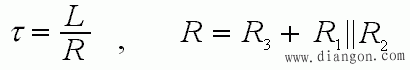
可见：时间常数中 R 是从 L 两端看进去的等效电阻，L / R 即为时间常数。

② 初始电流 i_L( 0₊ ) 的作用

如果令初始输入为 0，即：

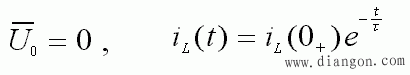
可见：只有动态元件 L 的初始储能产生的响应。

③ 电流的稳态值 i _L(∞)

如果 L 的初始储能为零，有：

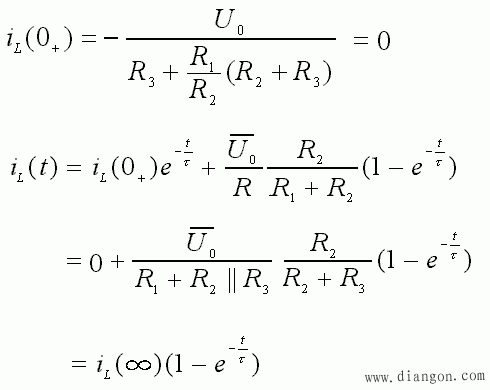
可见：只有初始输入产生的响应。

重要结论：电路的全响应是电路的零输入响应和零状态响应的线性叠加！其形式为：

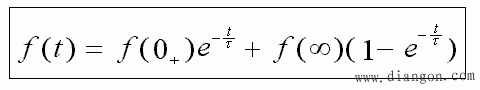
因此，只要计算出 τ、f (0₊ )、f (∞) 三个值代入公式即得电路的全响应。这三个值被称为“动态电路三要素”。