- 分析动态电路中的电参量如电流、电压时,必须将其表示成一个随时间变化的函数。
实际上,在某个时刻,将开关闭合或断开,就可表示成一个函数。
1、Unit-step Function 单位阶跃函数
- 在 t = t 0 时刻,将直流电压源 U 0 与电路接通,可表示成:
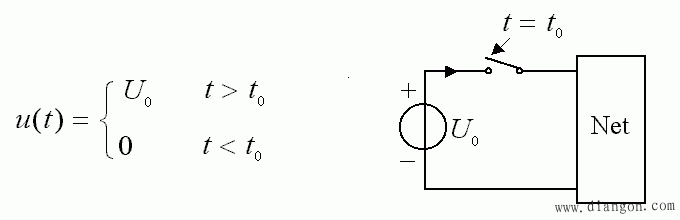
- 定义一个名为“单位阶跃函数”:
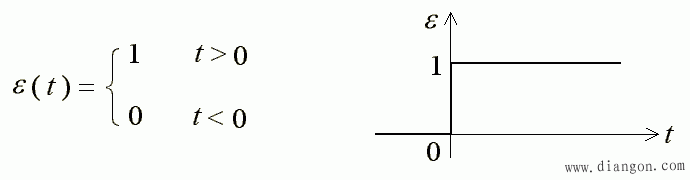
- 函数在 t = 0 时,发生了跃变。但为了问题的方便,认定:
ε ( t = 0+ ) = 1
显而易见:ε ( t = 0- ) = 0
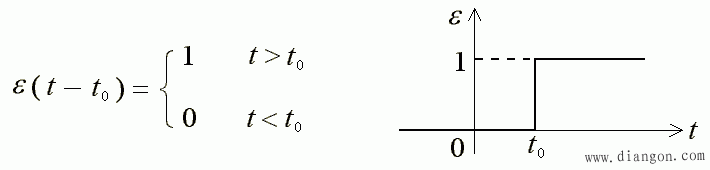
- 只要令 t' = t - t0 即可。
上述直流电源的开关例子可表示为:
u( t )= u0 ε ( t - t0 )
一个幅度为 I0 的矩形脉冲,可以用单位阶跃函数表示成:
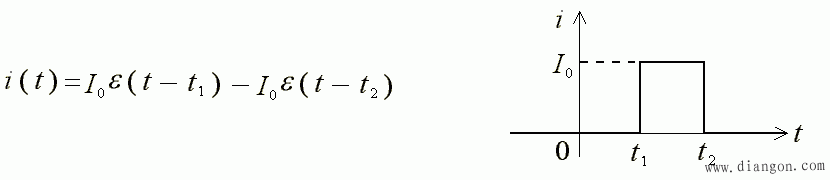
2、Unit-impulse Function 单位冲激函数
- 单位冲击函数是另一个奇异函数,用 δ (t) 表示,其定义为:
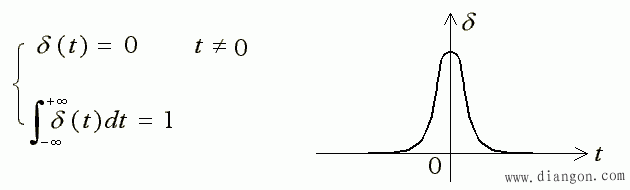
- 由定义可见, δ(t)只存在于 t = 0 时刻,故有:
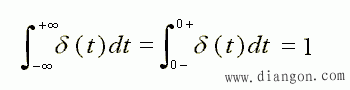
- δ(t)的性质有:
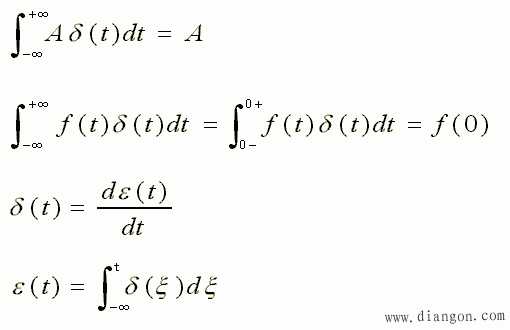
- δ(t) 与 ε(t) 的关系证明如下:
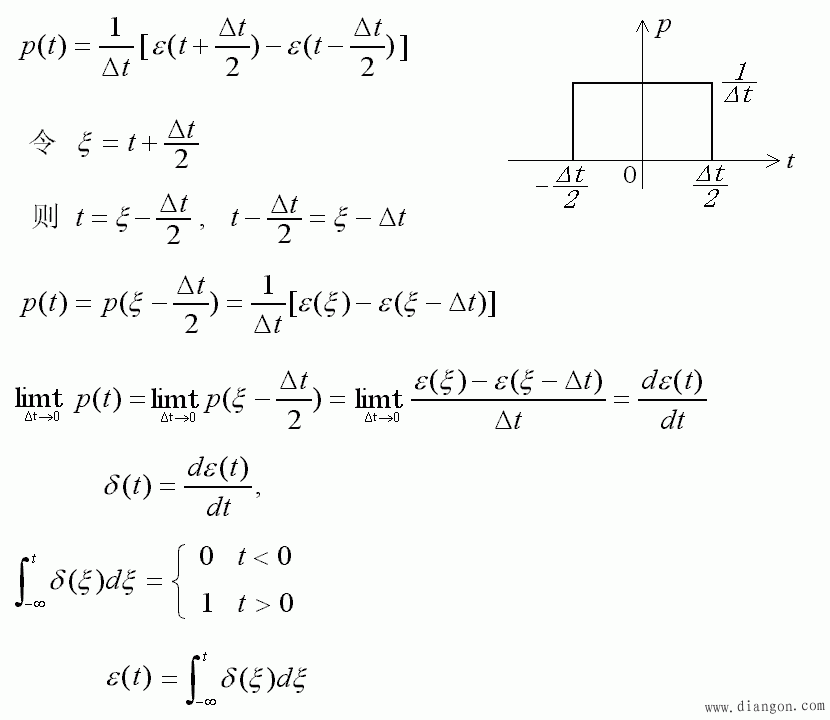
- 例如:如果在 t = 0 时刻,将恒压源 U0 加到一个事先没有电荷的电容 C 上,则有:
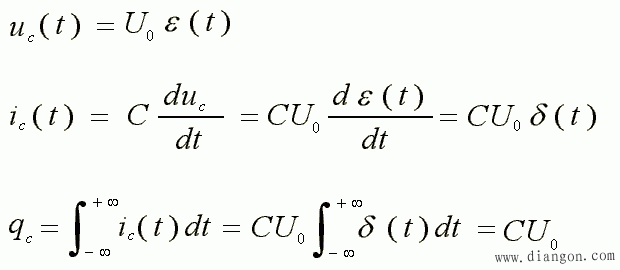
- 得结论:
- 充电前后,电容电压发生跃变 0→U0;
- 流过电容的电流为冲激电流 CU0δ(t);
- 电容极板上的电荷量的跃变是有限的,为冲激电流的强度 CU0。
- 又例如,如果在 t = 0 时刻,将恒流源 I0 加到一个事先没有电流的电感 L 上,则有:
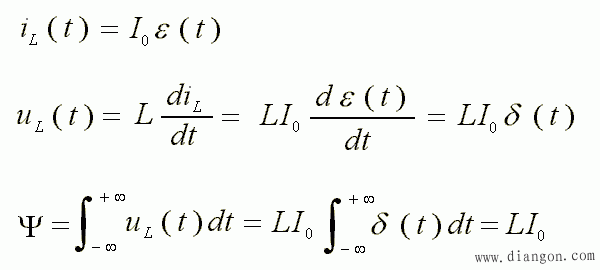
- 得结论:
- 给电感接上恒流源前后,迫使电感电流发生跃变 0→I0;
- 电感两端产生的感应电动势为冲激电压 LI0δ(t);
- 电感中的磁匝链数的跃变是有限的,为冲激电压的强度 LI0。
