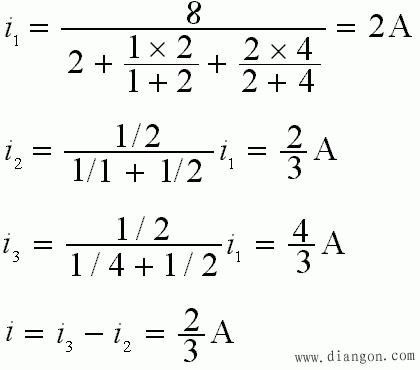1、互易定理的内容
- 在网孔电流法中,有互阻 R ij = R ji ,在节点电压法中,有互导 G ij = G ji ,这一现象已经向我们暗示出电路中一条重要性质-互易性。
互易定理则描述了线性电阻电路中的激励与响应的可互换性。
对于一个仅含线性电阻的电路,在单一激励下产生的响应,当激励和响应互换位置时,其比值保持不变。
1.1 互易定理的第一种形式
- 对于一个线性电阻电路,单一电压源 U s 在 1-1’支路中作用,而在 2-2’支路中产生了电流 i 2 , i 2 的值等于将电压源 U s 移到 2-2’支路上作用,在 1-1’支路中产生的电流 i1 的值。电流电压方向选关联参考方向。
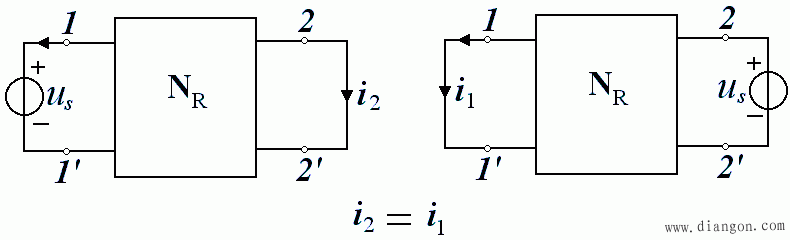
1.2 互易定理的第二种形式
- 对于一个线性电阻电路,单一电流源 i s 在 1-1’支路中作用,而在 2-2’支路中产生了电压 u 2 , u 2 的值等于将电流源 i s 移到 2-2’支路上作用,在 1-1’支路中产生的电压 u1 的值。电流电压方向选关联参考方向。
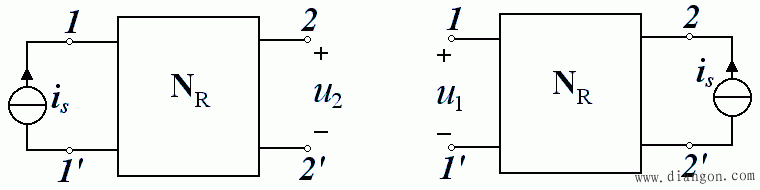
1.3 互易定理的第三种形式
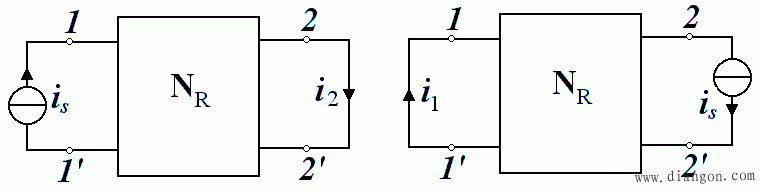
- 对于一个线性电阻电路,单一电流源 i s 在 1-1’支路中作用,而在 2-2’支路中产生了电流 i 2 , i 2 的值等于将电流源 i s 移到 2-2’支路上作用,在 1-1’支路中产生的电流 i1 的值。电流电压方向选关联参考方向。
2、互易定理的证明
- 如下图所示,两电路图中的 NR 完全相同,因此两电路的图(Graph)相同,所不同的是 1-1’和 2-2’ 支路中的内容不同。
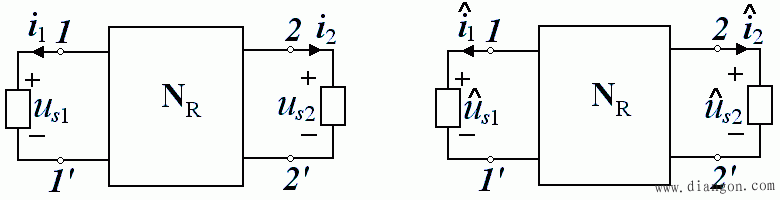
- 应用特勒根似功率定理,有:
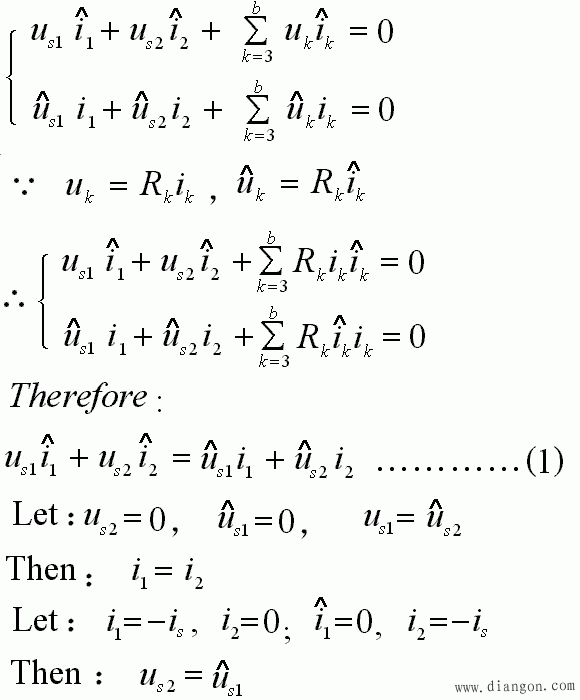
- 互易定理第三种表述的证明读者自便。
3、互易定理的应用
- 电路如图所示,求电流 i。
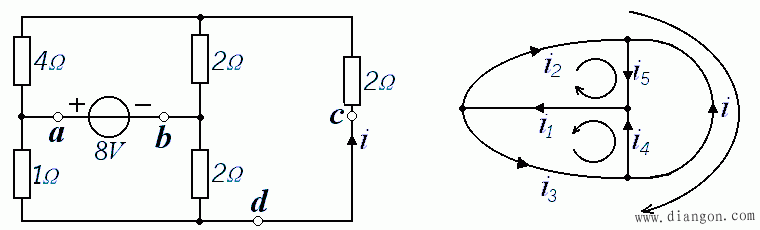
- 如果用支路电流法求解:b=6 ,n=4 , 要写出 b=6 个方程:3个节KCL方程+3个回路KVL方程
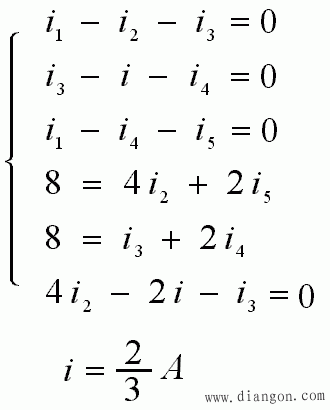
- 再用互易定理,原电路图可改化如下:
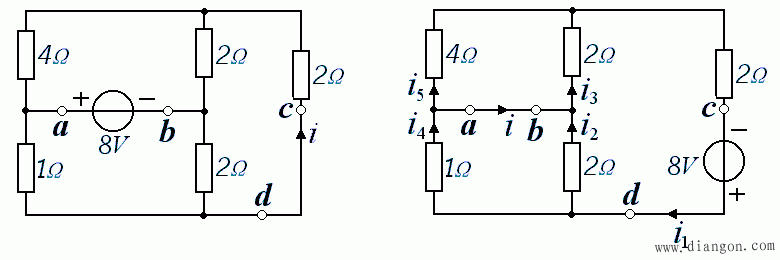
- 计算如下: