拉普拉斯反变换的部分分式展开

1．拉普拉斯反变换法
　　 用拉氏变换求解线性电路的时域响应时，需要把求得的响应的拉氏变换式反变换为时间函数。由象函数求原函数的方法有：
　　1） 利用公式
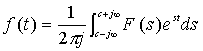
　　2) 对简单形式的 F(S) 可以查拉氏变换表得原函数
　　3) 把 F(S) 分解为简单项的组合，也称部分分式展开法。
　　　　　
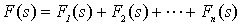
　　　　 则 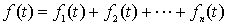　2.部分分式展开法
　　用部分分式法求拉氏反变换(海维赛德展开定理)，即将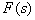展开成部分分式，成为可在拉氏变换表中查到的 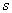的简单函数，然后通过反查拉氏变换表求取原函数。
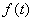　　设 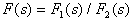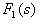，的阶次不高于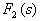的阶次，否则，用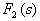除 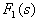，以得到一个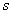的多项式与一个余式（真分式）之和。部分分式为真分式时，需对为分母多项式作因式分解，求出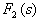=0的根。
　　设象函数的一般形式：
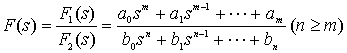
　　即 F（s）为真分式。下面讨论 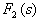=0 的根的情况。
　　1） 若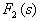=0 有 n 个不同的单根 p₁、p₂……p_n 。利用部分分式可将F(s)分解为：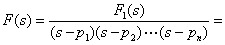
　　　
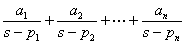
　　　 待定常数的确定：
　　　 方法一：按 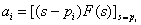， i =1, 2, 3, … , n 来确定。
　　　 方法二：用求极限方法确定a_i的值
　　　　　
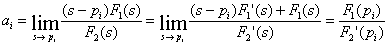
　　 得原函数的一般形式为：
　　　　　
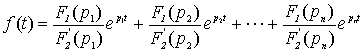
　　2） 若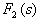=0有共轭复根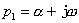和 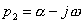，可将F(s)分解为：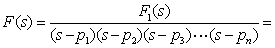
　
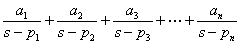
　　 则，
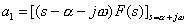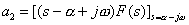
　因为F(s)为实系数多项式之比，故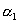和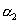为共轭复数。设，
　　　　　
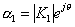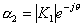
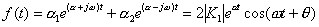
　　3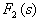） =0 的具有重根时，因含有 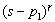的因式。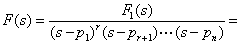
　　　　　
　　　　
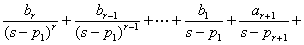
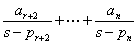
　　　 则， ； ； …… ；
　　　　　　
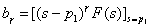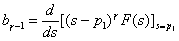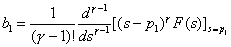
　　总结上述得由 F(s) 求 f( t) 的步骤：
　　 1） n = m 时将 F(s) 化成真分式和多项式之和；
　　 2） 求真分式分母的根，确定分解单元；
　　 3） 将真分式展开成部分分式，求各部分分式的系数；
　　 4） 对每个部分分式和多项式逐项求拉氏反变换。