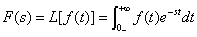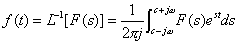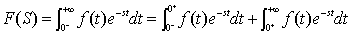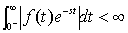来源:本站
导读:目前正在解读《拉普拉斯变换法》的相关信息,《拉普拉斯变换法》是由用户自行发布的知识型内容!下面请观看由(
电工学习网 - www.9pbb.com)用户发布《拉普拉斯变换法》的详细说明。
拉普拉斯变换法是一种数学积分变换,其核心是把时间函数
f(t) 与复变函数 F(s) 联系起来,把时域问题通过数学变换为复频域问题,把时间域的高阶微分方程变换为复频域的代数方程,在求出待求的复变函数后,再作相反的变换得到待求的时间函数。由于解复变函数的代数方程比解时域微分方程较有规律且有效,所以拉普拉斯变换在线性电路分析中得到广泛应用。
拉普拉斯变换的定义
一个定义在 [0,+∞) 区间的函数
f(
t) ,它的拉普拉斯变换式
F(
s) 定义为
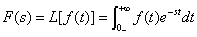
式中s=σ+
jω为复数,被称为复频率;
F(s)为
f(t)的象函数,
f(t)为
F(s)的原函数。
由
F(s) 到
f(t) 的变换称为
拉普拉斯反变换,它定义为
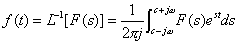
式中
c 为正的有限常数。
注意:
1)定义中拉氏变换的积分从
t=0- 开始,即:
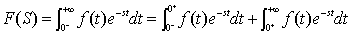
它计及
t=0- 至 0+ ,
f(
t) 包含的冲激和电路动态变量的初始值,从而为电路的计算带来方便。
2)象函数
F(s) 一般用大写字母表示, 如
I(s),
U(s) ,原函数
f(t) 用小写字母表示,如
i(t),
u(t)。
3)象函数
F(s) 存在的条件:
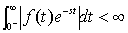
提醒:《拉普拉斯变换法》最后刷新时间 2023-07-10 03:56:30,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《拉普拉斯变换法》该内容的真实性请自行鉴别。