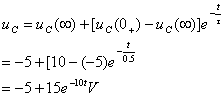RC电路同时具有初始储能和电源激励条件下的响应称作电路全响应。计算电路全响应与计算零状态响应一样,都可通过求解电路的微分方程得出,也可以用“三要素法”进行分析,不同的只是电路有初始储能。用“三要素法”通常更加方便,下面的例子用“三要素法”进行分析。
例1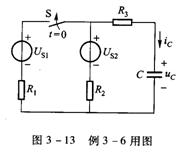 电路如图3-13所示,
电路如图3-13所示,![]()
![]()
![]() 时已处于稳态。
时已处于稳态。![]() 时开关闭合,试求电容元件两端电压
时开关闭合,试求电容元件两端电压![]() (t)和电流
(t)和电流![]() 。
。
解:![]() 时已处于稳态,
时已处于稳态,
即电容的初始电压为换路前电容的开路电压
uC(0-)=![]()
根据换路定律,电容电压的初始值uC(0+)=uC(0-)=6V
t=![]() 时,稳态值
时,稳态值![]() 为换路后电容的开路电压,因此
为换路后电容的开路电压,因此
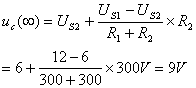
时间常数![]() ,其中R为换路后的电路从电容端看无源二端网络的等值电阻。
,其中R为换路后的电路从电容端看无源二端网络的等值电阻。
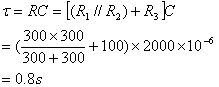
![]()
![]() +
+![]()
![]()
=![]()
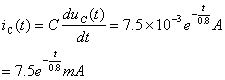
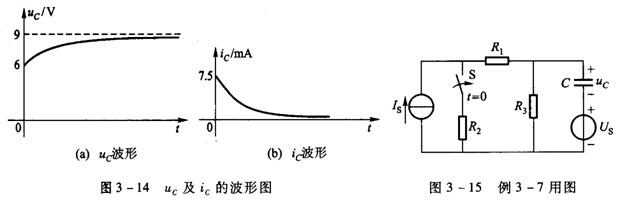
uC及iC的波形图如图3-14所示。
例2电路如图3-15所示,![]()
![]() 换路前已处于稳态,
换路前已处于稳态,![]() 时开关闭合,试求换路后(
时开关闭合,试求换路后(![]() )的
)的![]() 。
。
解:换路前(![]() )时
)时
![]()
换路后 ![]()
达稳定![]() 时
时
![]()
时间常数
![]()
于是