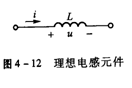
设电感L的端电压与电流采用关联参考方向，如图4-12所示。
设正弦电流
通过电感时，其端电压为:
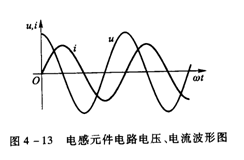
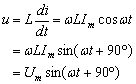
式中Um电感电压的最大值，由此可知电感电压和电流是同频率的正弦量，电压在相位上超前电流90°,其波形如图4-13所示。电感上电流、电压的有效值和初相位的对应关系为
电流、电压用有效值时关系为:
令
XL=ωL=2πfL
则 
或
XL具有电阻的量纲，称为感抗。当L的单位为H，ω的单位为rad/s时，XL单位为Ω。
电流、电压的关系可用相量式表达为:
或
 |
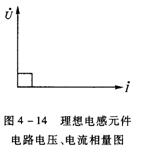
以上相量式同时体现了电感电流、电压之间的幅值关系和相位关系。相量图如图4-14所示。
知道了电压u与电流i的变化规律，便可计算出电路中的功率，电感电路的瞬时功率为:
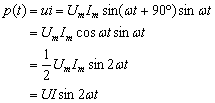
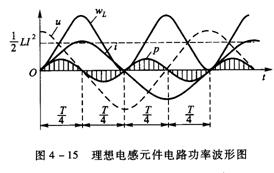
电感电路的瞬时功率也以正弦的规律变化，且变化频率为电流的两倍，如图4-15所示。平均功率为:
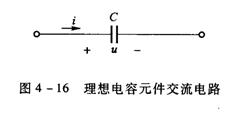
平均功率等于零表明理想电感是不消耗能量的，它只是与外电路或电源进行能量交换。这种能量交换的大小，可用瞬时功率的最大值进行衡量，并称其为电感的无功功率QL，因此 QL=ULIL=XLIL2
无功功率的单位是乏（var）或千乏（kvar）。
图4－15也画出电感的储能波形
，图上所标的
是电感元件的平均储能。