一阶RL电路也是以种常用的电路,一阶RL电路暂态过程的分析方法和一阶RC电路一样可用经典法和三要素法。
1、经典法
图3-16所示电路,t=0时开关S闭合,产生过渡过程。根据KVL,得回路电压方程为
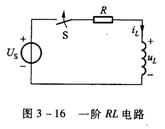
![]()
而:![]()
从而得微分方程:
![]() 或
或
![]()
此微分方程的通解为两个部分:一个是特解![]() ,一个是齐次方程式的解
,一个是齐次方程式的解![]() ,即
,即
![]()
特解可以是满足方程式的任何一个解,取t=![]() 时电路的稳定分量,即
时电路的稳定分量,即![]() =
=![]() 。
。
微分方程的齐次方程式为:![]()
令其通解为![]() ,代入齐次微分方程式可得特征方程式是:
,代入齐次微分方程式可得特征方程式是:
![]()
所以,特征方程式的根为: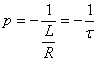
式中![]() ,其量纲为
,其量纲为![]() (秒),称为电路暂态过程的时间常数。
(秒),称为电路暂态过程的时间常数。
因此微分方程的通解
![]() =
=![]() +
+![]()
积分常数A需用初始条件来确定。在t=0时
![]() =
=![]() +
+![]() =
=![]() +A
+A
由此可得:A=![]() -
-![]()
 因此
因此![]()
![]() +
+![]()
![]()
上述利用微分方程进行求解分析一阶RL电路的暂态过程的方法称为经典法,经典法的分析步骤为:
(1)用基尔霍夫定律列出换路后电路的微分方程式。
(2) 解微分方程。
2、三要素法
通过经典分析法我们得到图3-16所示电路,暂态过程中电感电流为:
![]()
![]() +
+![]()
![]()
上述结果可归纳为 “三要素法”,式中只要知道稳态值![]() ,初始值
,初始值![]() 和时间常数
和时间常数![]() ,这“三要素”,则
,这“三要素”,则![]() 便被唯一确定。它适合于任何含一个一阶RL电路在阶跃(或直流)信号激励下的过程分析。
便被唯一确定。它适合于任何含一个一阶RL电路在阶跃(或直流)信号激励下的过程分析。
要注意一阶RL电路时间常数![]() 为
为![]() ,一阶RL电路仅有一个电感元件,L即为电感元件的电感量,而R为换路后的电路中除去电感后所得无源二端口网络的等效电阻。
,一阶RL电路仅有一个电感元件,L即为电感元件的电感量,而R为换路后的电路中除去电感后所得无源二端口网络的等效电阻。
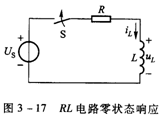
RL电路的零状态响应
当动态电路的初始储能为零(即初始状态为零)时,仅由外加激励产生的响应称作零状态响应。图3-17的一阶RL电路,设在开关S闭合前(t<0),电感L无初始储能,当t=0时,开关S闭合。下面用“三要素法”分析电路的响应。
电感L无初始储能,即电感的初始电流![]() =0。根据换路定律,电容电压的初始值
=0。根据换路定律,电容电压的初始值![]() =
=![]() =0。故电路为零状态响应
=0。故电路为零状态响应
t=![]() 时,稳态值
时,稳态值![]() 为换路后将电感看成短路的电流,因此
为换路后将电感看成短路的电流,因此
![]() =
=![]()
时间常数![]() ,根据“三要素法”
,根据“三要素法”
![]()
![]() +
+![]()
![]()
=![]()
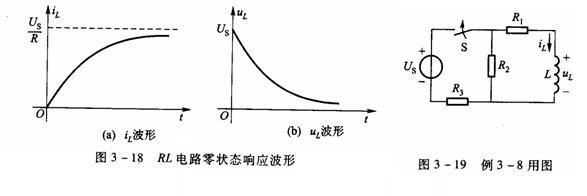
![]() 的变化曲线如图3-18(a)所示。
的变化曲线如图3-18(a)所示。![]() 按指数规律随时间增长而趋于稳态值
按指数规律随时间增长而趋于稳态值![]() 。
。
![]() =
=![]()
![]() 的变化曲线如图3-18(b)所示。图中电感电压是正值,这是电流上升产生的反电势。
的变化曲线如图3-18(b)所示。图中电感电压是正值,这是电流上升产生的反电势。
例3-8
电路如图3-19所示,![]()
![]() 换路前
换路前
已处于稳态,![]() 时开关闭合,试求换路后(
时开关闭合,试求换路后(![]() )的
)的![]()
![]() 。
。
解:![]() 时已处于稳态,
时已处于稳态,
即电感的初始电流为换路前电感电流
![]() =
=![]() =0
=0
t→![]() 时,稳态值
时,稳态值![]() 为换路后将电感看成短路的电流,因此
为换路后将电感看成短路的电流,因此
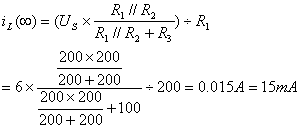
时间常数![]() ,而R为换路后的电路从电感看无源二端网络的等值电阻。
,而R为换路后的电路从电感看无源二端网络的等值电阻。
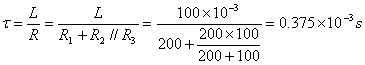
![]()
![]() +
+![]()
![]()
=15(1-![]() )mA
)mA
RL电路的零输入响应
一阶RL电路中,如果在换路的瞬间电感元件已储存有能量,那么即使电路中无外加激励电源,换路后,电路中的电感元件将通过电路释放储能,在电路中产生响应,即零输入响应。
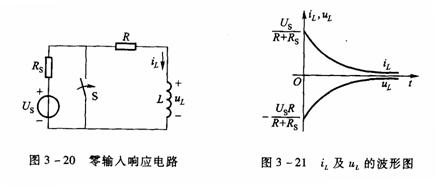
电路如图3-20所示,开关S原来断开,电路已经稳定。t=0开关S闭合,使电路产生过渡过程。此时,电感的初始电流为换路前电感的短路电流
![]() =
=![]()
根据换路定律,电感电流的初始值
![]() =
=![]() =
=![]() 。
。
t→![]() 时,稳态值
时,稳态值![]() 为换路后电感储能耗尽后的电流,因此
为换路后电感储能耗尽后的电流,因此![]() =0
=0
根据三要素法,得换路后电感的电流为:
时间常数![]()
![]()
![]() +
+![]()
![]()
=![]()
![]()
![]() =-
=-![]()
![]() 及
及![]() 的波形如图3-21所示。图上电感的端电压为负值,这是由电流衰减产生的反电势。
的波形如图3-21所示。图上电感的端电压为负值,这是由电流衰减产生的反电势。
例3-9
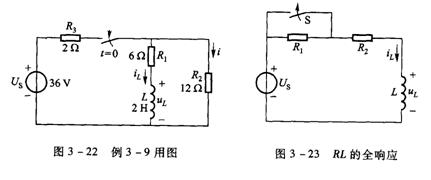
电路如图3-22所示,换路前已处于稳态,![]() 时开关断开,试求换路后(
时开关断开,试求换路后(![]() )的
)的![]()
![]() 。
。
解:![]() 时已处于稳态,
时已处于稳态,
即电感的初始电流为换路前电感的短路电流
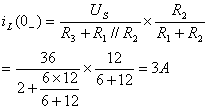
根据换路定律,电感电流的初始值![]() =
=![]() =3A。
=3A。
t→![]() 时,稳态值
时,稳态值![]() 为换路后电感储能耗尽后的电流,因此
为换路后电感储能耗尽后的电流,因此
![]() =0
=0
时间常数![]() ,而R为换路后的电路从电感端看无源二端网络的等值电阻。
,而R为换路后的电路从电感端看无源二端网络的等值电阻。
![]()
![]()
![]() +
+![]()
![]() =3
=3![]() A
A
![]() -
-![]() -3
-3![]() A
A
RL电路的全响应
电路如图3-23所示,在换路前电路为稳定状态,t=0时闭合开关S。
![]() 时已处于稳态,即电感的初始电流为换路前电感的短路电流
时已处于稳态,即电感的初始电流为换路前电感的短路电流
![]()
根据换路定律,电感电流的初始值
![]() =
=![]()
![]()
t→![]() 时,稳态值
时,稳态值![]() 为换路后电感的短路电流,因此
为换路后电感的短路电流,因此
![]()
![]()
时间常数![]() ,而R为换路后的电路从电感看无源二端网络等的值电阻。
,而R为换路后的电路从电感看无源二端网络等的值电阻。
![]()
![]()
![]() +
+![]()
![]()
![]() +
+![]() -
-![]()
![]()
例3-10
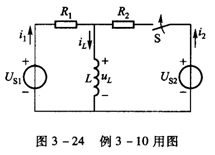 电路如图3-24所示,
电路如图3-24所示,![]()
![]()
换路前已处于稳态,![]() 时开关闭合,试求换路后(
时开关闭合,试求换路后(![]() )的
)的![]()
![]() 及
及![]() 。
。
解:开关S闭合前电感L中的电流
![]()
开关S闭合后各电流初始值
![]() 。
。
开关S闭合后电感电流的稳态值
![]()
求电路时间常数
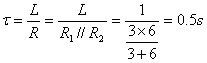
于是
![]()
![]() =6
=6![]() V
V
![]()
![]()
