正弦交流电可用三角函数式和波形图表示，但是用三角函数式和波形图在对电路进行分析计算往往比较复杂；正弦交流电还可用相量表示，相量表示法可简化分析计算。相量表示法是用复数表示正弦交流电的方法，因此相量表示法的基础是复数。
1、复数及其运算
在数学中，一个复数A可以表示成代数式、指数式或极坐标式，复数A也可以表示为复平面上的一个点或由原点指向该点的有向线段(矢量)，如图4-3所示。该有向线段的长度a称为复数A的模，模总是取正值。该有向线段与实轴正方向的夹角θ称为复数A的辐角。
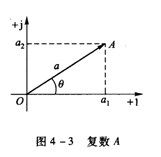
1、 代数式 A=a1+ja2
式中为复数单位；a1和a2分别为复数A的实部和虚部。
2、 指数式 A=aejθ
a和θ分别是A的模和辐角
3、极坐标式 A=a∠θ
复数代数式、指数式和极坐标式之间可以相互转换，复数代数式、指数式和极坐标式之间的转换关系为
和 
以及欧拉公式 
为简化计算，复数相加，可用代数式，两个复数相加减等于把它们的实部和虚部分别相加减。而两个复数乘除可用指数式和极坐标式。
例如，若
则两个复数相加 
两个复数相减 
两个复数相乘 
两个复数相除 
例1已知复数A=15∠-400，试把它变换为代数式。
解：A=15∠-400
=15cos400-j15sin400
=11.49-j9.64
代数式为 A=11.49-j9.64
例2复数 7+j2乘以16∠-300的积。
解：把7+j2变为极形：
θ= arctan2/7=15.950
所以 7+j2=
（7+j2）×16∠-300 =7.28∠15.950×16∠300
=7.28×16∠-300+15.950
=116.48∠14.050
2、正弦信号的相量表示
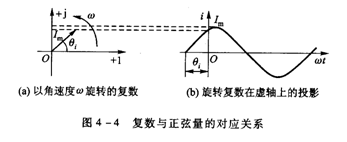
正弦信号由幅值、频率和初相位三个要素确定。由于在线性正弦稳态电路中，各处的电流和电压都是正弦信号，并且它们的角频率与正弦电源的角频率相同，因此，在进行正弦稳态电路分析时，对于正弦信号的幅值和初相位，是我们最为关心的两个要素。而对于一个复数可以由模和辐角来确定，例如一个复数Im∠θi ，令这个复数在复平面上以角速度ω逆时针旋转，如图4-4（a）所示，在任何时刻，这个复数在虚轴上的投影等于Imsin(ωt + θi )，如图4-4（b）所示，这正好是用正弦函数表示的正弦电流i。可见复数
Im∠θi与正弦电流i=Imsin(ωt + θi )有一种相互对应的关系，因此可用复数Im∠θi来表示正弦电流i，记为：
并称其为相量。复数的模和辐角恰好分别对应正弦电流的幅值和初相位。在此基础上，再考虑已知的角频率，就能完全表示一个正弦电流。像这样用来表示正弦信号的特定复数称为相量。为了将相量与一般复数相区别这种命名和记法是为了强调它与正弦量的联系，而在运算上与一般复数运算相同。符号Im上加“·”。
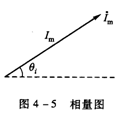
相量和复数一样, 它可以在复平面上用矢量表示,这种表示相量的图称为相量图。为了简练、醒目,相量图可省去坐标轴,如图4-5所示。另外，对于正弦电流
可表示为
也可表示为
,
称为电流的最大值相量，
称为电流的有效值相量。同样对于正弦电压
可表示为振幅相量
或有效值相量
要特别注意的是，正弦信号是时间的实函数，并非矢量或复数量，所以，相量不等于正弦信号。但是，它们之间有相互对应关系。
本书规定电压或电流相量乘以
后取其虚部还原成正弦函数
例如，已知角频率为ω的正弦电流的相量
， 那么该电流的表达式为
由于这种换算是约定俗成的，一般省去中间运算，直接写成
若是有效值相量，还原成正弦函数时需要乘以
。
又如，若正弦电压u=10sin(ωt-30°)V，则电压相量为 
或
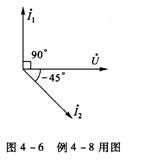
例3图4-6所示的是电压和电流的相量图，并已知U=220V，I1=10A,，I2=5 A，试分别用三角函数式及复数式表示各正弦量。
解：三角函数式：
相量式 
°V
°
°
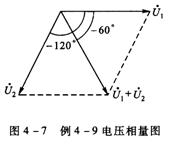
例4已知电压u1=10sinωt A, u2=10sin(ωt-120°)A，且u=u1+u2，试求u并画出电流的相量图。
解 : 由已知条件可得
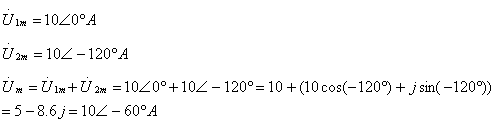
V
电压的相量图如图4-7所示
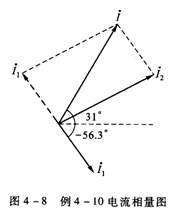
例5
=3.6∠-56.30 A，
=5.83∠310 A,求：
并画相量图。
解：变为代数式：
=3.6cos∠-56.30+j3.6sin∠-56.30=2-j3A
=5.83cos∠310+j5.83sin∠310=5+j3A
=（5+j3）-（2-j3）
=3+j6=6.7A∠63.40 A
电流的相量图如图4-8所示。