1.正弦量
正弦电流:随时间按正弦规律变动的电流。
正弦电压:按正弦规律变动的电压。
随时间t按照正弦规律变化的物理量,都称为正弦量,它们在某时刻的值称为该时刻的瞬时值,则正弦电压和电流分别用小写字母i、u表示。
2.正弦量的表达式
函数表示法:![]()
![]() —最大值(振幅、幅值),反映正弦量在整个变化过程中所能达到的最大值;
—最大值(振幅、幅值),反映正弦量在整个变化过程中所能达到的最大值;
![]() —相位,反映正弦量变动的进程;
—相位,反映正弦量变动的进程;
![]() —角频率(
—角频率(![]() ),反映正弦量变化的快慢。
),反映正弦量变化的快慢。
![]()
![]() —初相位,反映正弦量初值的大小、正负。
—初相位,反映正弦量初值的大小、正负。
![]() ,
,![]() ,
,![]() —正弦量的三要素。
—正弦量的三要素。
例如已知![]() ,则
,则![]() 。
。
3.有效值
周期电流![]() 和直流I分别通过相同的电阻R,若二者做功的平均效果相同,则将此直流I的量值规定为周期电流
和直流I分别通过相同的电阻R,若二者做功的平均效果相同,则将此直流I的量值规定为周期电流![]() 的有效值。
的有效值。
电流![]() 在微分时间dt内所作的功(即吸收的电能)
在微分时间dt内所作的功(即吸收的电能)
![]()
在一个周期T内做功为
![]()
量值为I的直流于同一时间T内所作的功为
![]()
根据上述有效值的概念应有![]() ,于是得到
,于是得到
![]()
正弦电流属于周期电流。将式正弦电流表达式代入得到电流的有效值
![]()
即正弦电流的有效值等于其振幅乘以![]() 。
。
4.相位差
设![]() ;
;![]()
则u(t)与i(t)的相位差![]() 对两个同频率的正弦量来说,相位差在任何瞬时都是一个常数,即等于它们的初相之差,而与时间无关。φ的单位为rad(弧度)或(度)。主值范围为|φ|≤π。
对两个同频率的正弦量来说,相位差在任何瞬时都是一个常数,即等于它们的初相之差,而与时间无关。φ的单位为rad(弧度)或(度)。主值范围为|φ|≤π。
如果φ=ΨuΨi>0 (如下图),则称电压u的相位超前电流i的相位一个角度度φ,简称电压u超前电流i角度φ,意指在波形图中,由坐标原点向右看,电压u先到达其第一个正的最大值,经过φ,电流i到达其第一个正的最大值。反过来也可以说电流i滞后电压u角度φ。
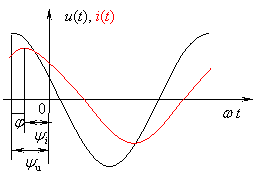
如果φ=ΨuΨi<0,则结论刚好与上述情况相反,即电压u滞后电流i一个角度|φ|,或电流i超前电压u一个角度|φ|。
又设 ![]()
(1)![]() 当
当![]() ,则
,则![]() ,
,![]() 与
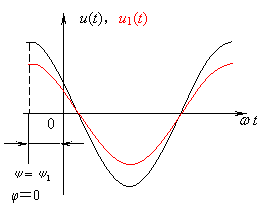
与![]() 同相。如下图
同相。如下图
φ=ΨuΨi=0。
(2)![]() 当
当![]() ,
,![]() ,
,![]() 与
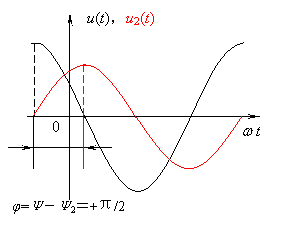
与![]() 正交。如下图(这里φ=Ψ-Ψ2=+π/2)
正交。如下图(这里φ=Ψ-Ψ2=+π/2)
(3)![]() 当
当![]() ,
,![]() ,
,![]() 与
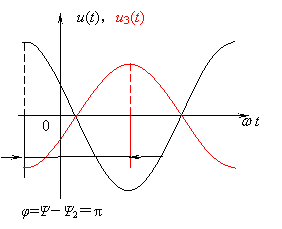
与![]() 反相。
反相。
2) 函数表达式前的正、负号要一致。当![]() 。
。
3) 当两个同频率正弦量的计时起点(即波形图中的坐标原点)改变时,它们的初相也跟着改变,但它们的相位差却保持不变。所以两个同频率正弦量的相位差与计时起点的选择无关。
