1、定义：用一条折线来分段逼近特性曲线，所以有时也称为折线法。
2、电路模型：
若流控电阻的特性为：
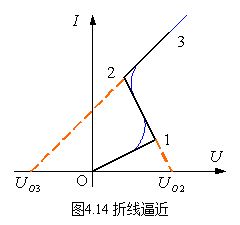
则用O1、12和23段直线来表示为：
—第k段直线与U轴交点的坐标。
—第k段直线的斜率：
它具有电阻的量纲，称为动态电阻。
模型通常有以下两种等效方式
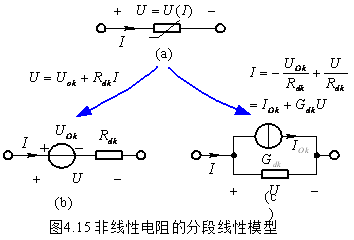
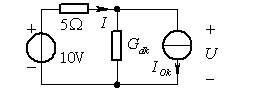
例题4.5：试用分段线性近似法解图(a)电路，其中非线性电阻的特性由图(b)曲线表示。
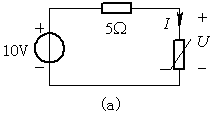
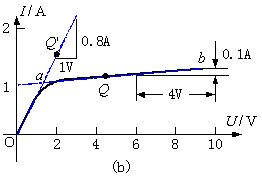
图4.16 例题4.5
解：非线性电阻的特性可用O-a, a-b两条直线分段逼近。取U为自变量，直线方程是
式中
，称为动态电导。
当
时，取O-a段，该段通过原点，
当
时，取a-b段，
。其分段线性模型如图示。由节点法得
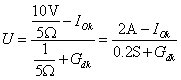
对应O-a段
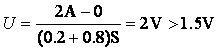
所以这是一个虚解，该点落在
点。
对应a-b段，
V，在a-b段内，得
。这便是近似解答，在图上位于Q点。
注：如果电路中有多个非线性电阻元件，可以分别求出它们的分段线性模型。对每个非线性电阻取出一个区段进行组合，得到多种区段组合的线性电路。对于某一区段组合，只有全部非线性电阻的解都分别位于该组合的区段以内时，才是真正的解答。只要有一个超出范围，便是虚解。