1、定义:数值分析法是借助计算机计算得出电路方程的数值结果而非解析表达式。
2、原理:
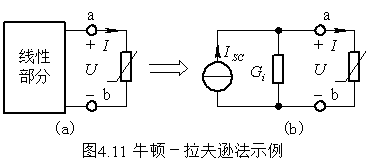
I=I(U) (1)
图(a) a,b左端的线性含独立源一端口网络可以等效成诺顿电路,如图(b)。线性部分端口特性为 I=I---sc-–GiU (2)
其中I---sc-是端口的短路电流,Gi是一端口网络的等效内导。将式(1)代入式(2),得I(U)–I---sc + GiU=0 (3)
求解电路,归结为求式(3)的根。但这是一个变量U的非线性方程,一般不易求解。牛顿-拉夫逊法的思路是:若令 ![]() (4)
(4)
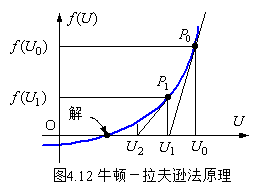
在![]() 坐标平面上画出f(U)与U的关系曲线,如图4.12。则它与横坐标U的交点就是方程(3)的解答。现利用图4.12说明牛顿-拉夫逊法的计算过程:先假设一电压值
坐标平面上画出f(U)与U的关系曲线,如图4.12。则它与横坐标U的交点就是方程(3)的解答。现利用图4.12说明牛顿-拉夫逊法的计算过程:先假设一电压值![]() (称为初值)代入式(4)求出
(称为初值)代入式(4)求出![]() ,对应图4.12坐标上的
,对应图4.12坐标上的![]() 点。一般情况下
点。一般情况下![]() ,说明初值不是方程的解答。然后在
,说明初值不是方程的解答。然后在![]() 点作切线,该切线与U轴的交点记作
点作切线,该切线与U轴的交点记作![]() ,
,![]() 比
比![]() 更接近方程的解答。再用
更接近方程的解答。再用![]() 代替
代替![]() 重复上述过程得到
重复上述过程得到![]() ……。
……。
在![]() 坐标平面上画出f(U)与U的关系曲线
坐标平面上画出f(U)与U的关系曲线
3、牛顿-拉夫逊法的计算过程:
1) 设一电压值![]() (初值)代入式(4)求出
(初值)代入式(4)求出![]() ,对应图4.12坐标上的
,对应图4.12坐标上的![]() 点;
点;
2) 在![]() 点作切线,该切线与U轴的交点记作
点作切线,该切线与U轴的交点记作![]() ,
,![]() 比
比![]() 更接近方程的解;
更接近方程的解;
3) 用![]() 代替
代替![]() 重复上述过程得到序列:
重复上述过程得到序列:![]() 其中:
其中:
![]() ,
,![]()
4) 判断相继两次迭代值的绝对误差是否在容许误差(说明定义)范围之内,即
![]()
成立,则结束
注:说明不成立情况。
i当有多解时难以求出全部解;
ii对初值敏感易发散;
iii当接近解时收敛很快。
例题4.4:试用牛顿-拉夫逊法求解图4.13所示P-N结二极管电路。二极管特性为:![]() ,其中
,其中![]() 。又已知
。又已知![]() 。规定容许误差
。规定容许误差![]() V。
V。

解:列出回路电压方程:
![]() (1)
(1)
代入二极管特性得
![]() (2)
(2)
令
![]() (3)
(3)
求导数得
![]() (4)
(4)
由递推公式及式(3)、(4)得迭代公式:
 (5)
(5)
选取初值![]() 。二极管正向导通时两端电压一般小于0.8V,取
。二极管正向导通时两端电压一般小于0.8V,取![]() ,迭代过程列于下表:
,迭代过程列于下表:
表4.1 例题4.4的迭代过程
|
|
|
| |
0 | 0.3000 | 0.2565×10-3 | -3.392×101 | 51.31 |
1 | 0.3661 | 3.2610×10-3 | 1.200×101 | 640.7 |
2 | 0.3474 | 1.5869×10-3 | 3.441 | 312.3 |
3 | 0.3364 | 1.0388×10-3 | 6.340×10-1 | 240.8 |
4 | 0.3333 | 9.2213×10-4 | 3.612×10-2 | 181.9 |
5 | 0.3330 | 9.1511×10-4 |
得近似解
![]()
