1.正弦电流电路的功率
吸收瞬时功率
平均功率：瞬时功率在一个周期内的平均值（有功功率），即
为功率因数
2.RLC元件上的功率
1）电阻元件：电阻
上，
与
同相位，
，故
瞬时功率 
平均功率 
2）电感和电容元件：感抗或容抗（即电抗）上
与
相位正交，
，功率因数
瞬时功率 
平均功率 
注：维持电感的正弦电压和电流不需要消耗其它能量。
3.无功功率
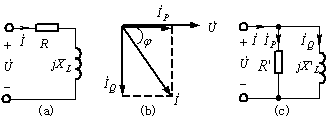
与电压
同相位的电流分量，故产生平均功率。因此把
称为电流
的有功分量
与电压
正交,不产生平均功率。故
称为电流
的无功分量。
定义无功功率
元件上的无功功率：
1) 电阻元件 QR = 0
2) 纯电感的无功功率为 
3) 纯电容的无功功率为 
4.视在功率
也称（表观功率）表征某些电气设备的容量。
,
,
故P、Q、S三者之间的关系为
上述关系也可用三角形来表示，如图，称为功率三角形。
也称功率因数角
5.无功补偿
工程上的负载多为感性，为提高功率因数可在感性负载两端并联电容器
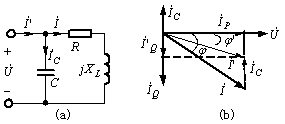
端口电流的无功分量却因并联电容而减小到
上式乘以端口电压便得到 
因此，补偿后 
例1 在工频条件下测得某线圈的端口电压、电流和功率分别为100V、5A和300W.求此线圈的功率因数、等效电阻和等效电感。
解：由式求得功率因数
线圈电阻、感抗和电感分别为
0.051H
例2 图(a)所示电路，感性负载Z接于220V、50Hz正弦电源上，负载的平均功率和功率因数分别为2200W和0.8。(1) 求并联电容前电源电流、无功功率和视在功率。(2) 并联电容，将功率因数提高到0.95，求电容大小、并联后电源电流、无功功率和视在功率。
解：(1) 并联电容前电源电流等于负载电流
负载功率因数角 
电源无功功率等于负载无功功率 
var
电源视在功率 
VA
(2) 并联电容后功率因数角为 
并联电容后电源提供的有功功率不变，无功功率为 
var
电源无功功率的差值等于电容上的无功功率 
var
由电容无功功率的计算公式得所需并联电容为
μF
并联电容后的电源视在功率 
VA
电源电流 
A