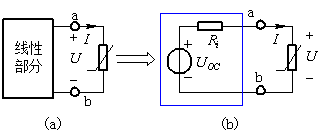
图1 对线性部分进行等效
端口左边的线性部分化简成戴维南(或诺顿)等效电路，其端口方程
U、I须满足非线性电阻的特性曲线。绘制两条曲线：
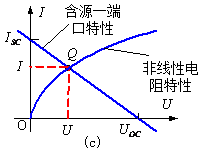
图2 简单电路的图解法原理
它们的交点Q，Q点的坐标
就是端口电压、电流的解答
I 当特性以曲线形式给出时用此方法
II 适用于简单非线性电路
III 直观但不精确
IV 原理是列出成对方程，在同一坐标系上特性曲线相交
例题1：图示为分析张弛振荡器工作点的电路。设图中电压源US＝9V，非线性电阻为氖管，其特性曲线如图(b)所示。(1)要求将电路的工作点设计在Q1和Q2之间(即负斜率段)，问电阻R的取值范围怎样？(2)若电阻R=1.5kΩ，求此时非线性电阻电压U和电流I。
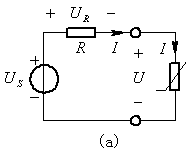
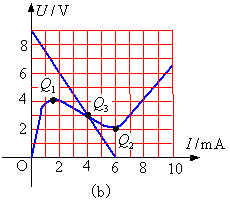
图3 例题1
解： (1) 由图(b)可见，Q1点电流I1＝1.5mA，电压U1＝4V。当工作点位于Q1时，电阻R须满足
Q2点电流I2=6mA，电压U2=2V。当工作点位于Q2时，电阻R须满足
所以当电阻
满足
时工作点位于
和
之间。
(2) 当R＝1.5kΩ时，线性部分的特性方程为
它在电压轴与电流轴上的截距分别为
V、
。在图(b)上画出此直线，它与非线性电阻特性曲线交于
点，从图中可以读出该点电压为
，电流
。