例1 设图 (a)电路中
，
，
，
，
。求电流
。
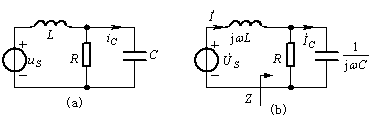
解：将图(a)中时域电路模型变换为相量模型，如图(b)，其中
。
仿照线性直流电路的计算，图(b)中RC并联部分的等效阻抗及总电流
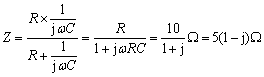
由分流公式得
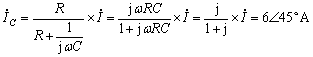
由相量和正弦量的变换关系得待求电流的时间函数
列写图所示电路的回路电流方程。
解：图示电路有两个独立回路。将直流电路的回路电流方程推广成相量形式。
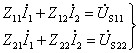
方程中
和
分别称为回路1(
所在回路)和回路2(
所在回路)的自阻抗；
和
称为回路1与回路2之间的互阻抗；
和
分别为回路1和回路2的源电压相量。自阻抗、互阻抗和回路源电压相量的列写规则与对直流电路列写自阻、互阻和回路源电压的规则相同。由此列出图题所示电路回路电流方程：
(
j
+
)
+
=
+(
)
=
例3 列写图所示电路的节点电压方程。
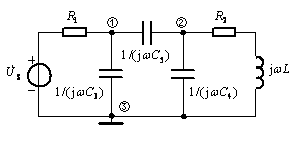
解：图示电路有三个节点，取节点③为参考点，其余两节点的节点电压相量分别用
和
表示，则所列节点方程的相量形式为
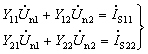
式中
和
分别称为节点①和节点②的自导纳；
和
称为节点①和节点②之间的互导纳；
和
分别称为流入节点①和节点②的源电流相量。列写自导纳、互导纳和节点源电流的规则与列写直流电路节点电压方程相应的规则是一样的。参照列写直流电路节点电压方程的方法列出图题所示电路的节点电压方程：
(
j
+ 
)
－j
=
－j
+(
+ j
+ j
)
=0
例4 图所示电路，当
时，电流
A。求当
时的电流
。
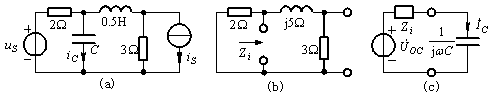
解：将图(a)电路化为相量形式的戴维南等效电路，如图(c)所示。由图(b)计算等效阻抗
由题给已知条件及图(c)计算等效开路电压
所以当
时，由图(c)得电容电流相量为
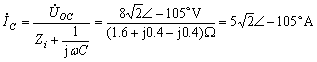
得电流瞬时表达式 
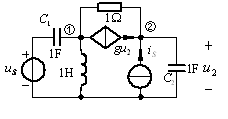
例5 已知图示电路中
，
，
，
。求受控电流源的电压
。
解：电压源和电流源的相量分别为
对节点①和②列相量形式节点电压方程
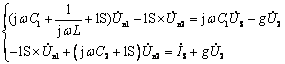
由图可知受控源控制量
解得 
受控电流源的电压为 
例6 在图(a)所示
移相电路中设
，试求输出电压
和输入电压
的相位差。
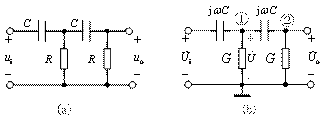
解：相量模型如图(b)所示。对节点①、②列节点电压方程：
联立解得
；又因为
，所以
，
即
越前于
的相位差为