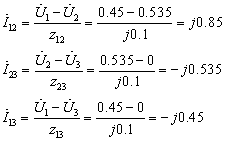三相短路电流的计算机算法

一、节点阻抗矩阵
n节点系统（n不包括参考节点）的节点电压方程为
　　
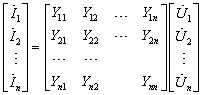
可以简写为：I_B=Y_BU_B　　　
两边同左乘Y_B^-1=Z_B，则节点电压方程变为：
　Z_BIB=U_B　
Z_B称为节点阻抗矩阵。
　　
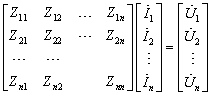
或
　　
可见，
　　对角元Z_ii称为自阻抗，其物理意义为：除节点i以外，其余节点都开路，在节点i注入单位电流时，节点i上的电压。因此， Z_ii等于从节点i向整个网络看进去的等值阻抗。
　　
可见，

　　非对角元Zij称为互阻抗，或称为转移阻抗，其物理意义为：除节点j以外，其余节点都开路，在节点j注入单位电流时，节点i上的电压。
显然， Z_ij=Z_ji
　　Z_B为没有零元素的对称矩阵。
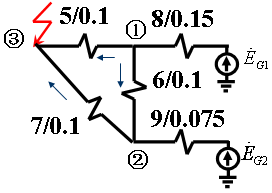
[例1]在图示电力系统中，发电机均为汽轮发电机；三条线路完全相同，长66km，电抗为x₁=0.4Ω/km。试求以标么值表示的节点阻抗矩阵。
　　
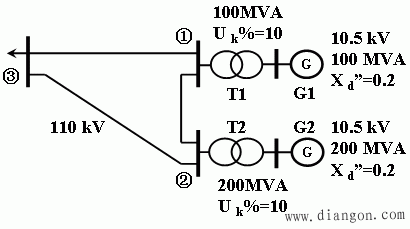
　　解：取功率基准值S_B=50MVA，各级电压基准值U_B=U_av=115、10.5kV，计算各元件的电抗标幺值，并做出等值电路。
　　

　　

　　
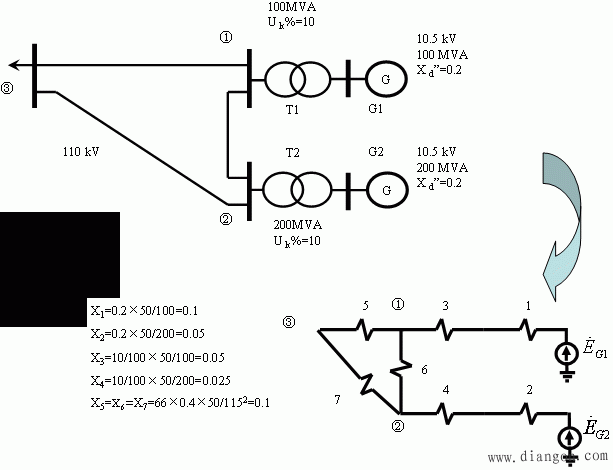
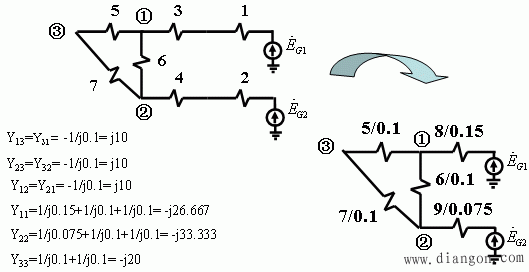
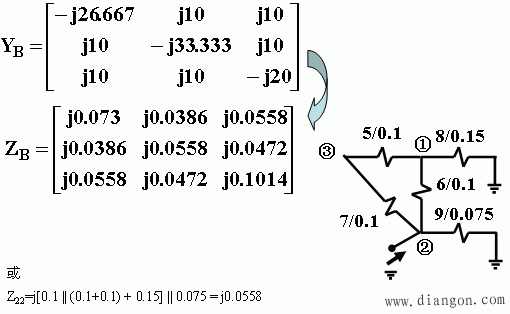
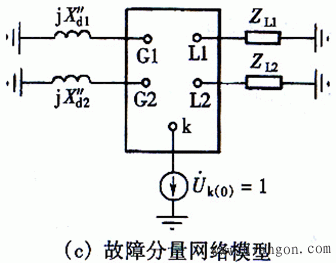
1、短路电流的网络计算模型
　 　　 　

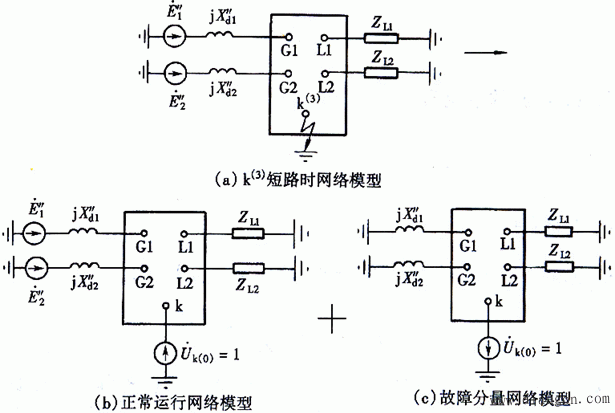
2、用节点阻抗矩阵计算三相短路电流
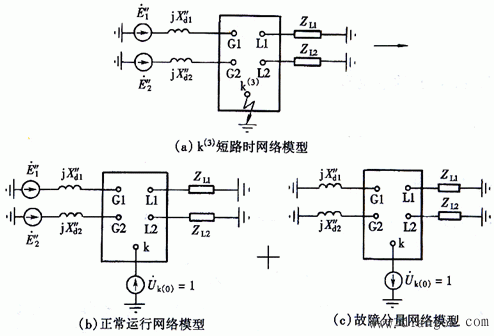
　　如果形成了节点阻抗矩阵Z_B，则Z_B中的对角元素Z_kk就是从节点k向整个网络看进去的等值阻抗。所以k点的三相短路电流（从k点流出）为：
　　
　　
　　

　　
　　
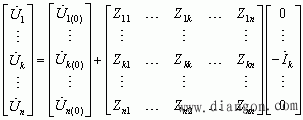
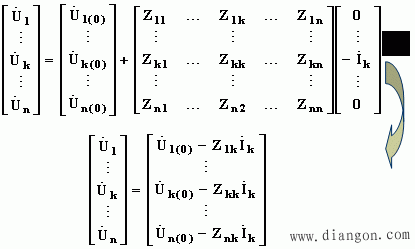
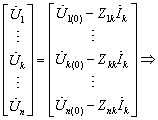
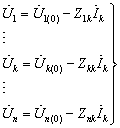　　 (8-44)
　　k点发生三相短路时，，所以，从k点流出的电流为：
　　 (8-40)
　　任意支路(i-j)的电流为：
　　　　 (8-45)
　　其中z_ij为i与j节点之间的支路阻抗。
　　

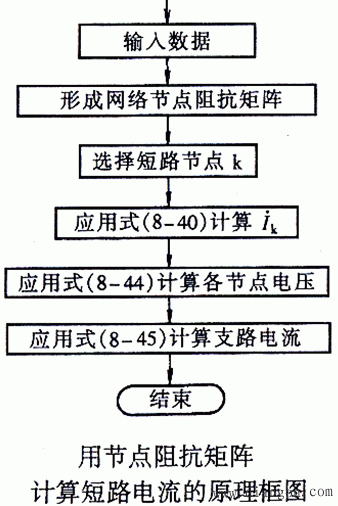
3、用节点导纳矩阵计算三相短路电流
　　在形成了节点阻抗矩阵Y_B后，则
　　Z_B=Y_B^-1，
　　或根据定义，在k点三相短路时，在节点k注入单位电流，其余节点的注入电流为零（即：开路），节点k上的电压即为节点k的自阻抗，其它节点上的电压即为各节点与节点k之间的互阻抗。
　　
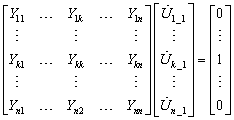
　　解出各节点电压后即可得到所需的自阻抗、互阻抗（转移阻抗）：
　　
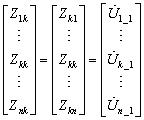
　　然后，计算过程同“7.2.2”节。
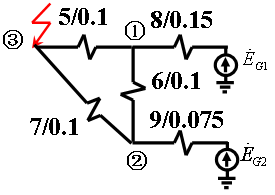
　　[例2]在例7-1中，③节点发生三相短路，试计算：
　　1）③节点的电流；
　　2）三个节点的电压；
　　3）三条线路中电流。
　　

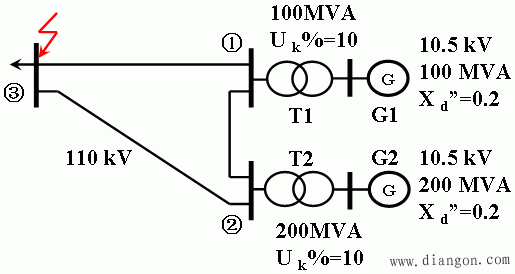
　　解：取功率基准值S_B=50MVA，各级电压基准值U_B=U_av=115、10.5kV，计算各元件的电抗标幺值，并做出等值电路。
　　

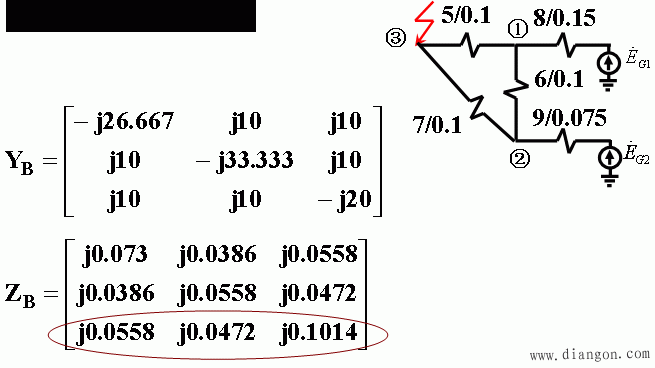
　　或
　　
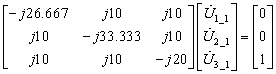
　　解上列线形方程组，求出各节点电压后，则可得到所需的自阻抗、互阻抗（转移阻抗）：
　　
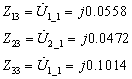
　　1）③节点的短路电流：
　　
　　
　　
　　2）三个节点的电压；
　　
　　3）三条线路中电流；