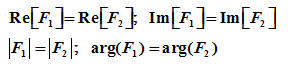复数的运算法则_复数的运算公式

（1）代数形式

共轭复数 F*=a-jb

在数学中虚单位常用i表示，如F=a+bi，但由于在电路中已用i表示电流，故虚单位改用j表示。

实部(real part)：Re[F] = a；虚部(imaginary part)：Im[F] = b。

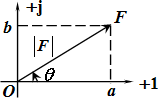
复数可用复平面上的向量表示(如图所示)。

（2）三角形式 F=|F|(cosθ+jsinθ)

|F|为复数的模，θ为复数的幅角，θ=argF。则

|F|=θ=arctan(b/a)。且a=|F|cosθ，b=|F|sinθ 。

（3）指数形式(exponential form)

（4）极坐标形式(polar form)

F=|F|<θ

2.复数的基本运算

（1）加减运算

复数的加减运算采用代数形式较为简便，或在复平面中使用平行四边形法则。设F₁ = a₁ + jb₁，F₂ = a₂ + jb₂，有

平行四边形法则：

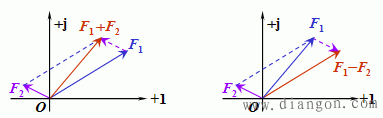
（2）乘除运算

复数的乘除运算使用指数形式或极坐标形式较为简便。

①指数形式

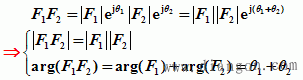
即复数乘积的模等于各复数模的积；辐角等于各复数辐角的和。

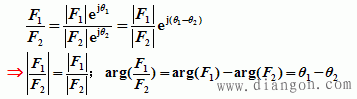
②极坐标形式

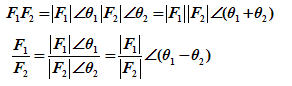
（3）旋转因子

复数 e^jθ = cosθ + jsinθ = 1∠ θ

Fe^jθ →复数F逆时针旋转一个角度θ ，模不变

+j ，–j， -1 都可以看成旋转因子。

若一个复数乘以j，等于在复平面上把该复数逆时针旋转π/2。若一个复数除以j ，等于把该复数乘以-j ，则等于在复平面上把该复数顺时针旋转π/2。

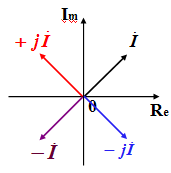
（4）相等运算

两个复数相等必须满足：

复数的实部、虚部分别对应相等；

或者复数的模和辐角分别对应相等。

若F₁ = F₂，则必须有

或