正弦量的三要素是指什么?

或

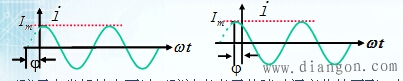
正弦量在坐标轴上可以正弦波来表示其随时间变化的图形，如上图。

三要素：

I_m:电流振幅 (amplitude) （最大值）

ω:角频率(angular frequency) （弧度/秒）

φ:初相位(initial phase angle)

正弦量一般用余弦函数来表示。

1.振幅与有效值

（1）瞬时值：正弦量在任一瞬间的值，用小写字母表示， 如i 、u。

（2）振幅：正弦量的最大值，用大写字母加下标“m”表示，如U_m、I_m。

（3）有效值(effective value)：用大写字母表示，如U、I。

在工程应用中常用有效值U、I表示交流电压、电流的大小：

①常用交流电表指示的电压、电流读数，就是被测物理量的有效值。

②标准电压220V，也是指正弦交流供电电压的有效值。

有效值定义：设两个相同的电阻，分别流过周期交流电流和直流电流。如果在周期信号的一个周期内，两个电阻消耗的能量相等，则该直流电流的数值为周期交流电流的有效值，表明两者在能量消耗方面具有相同的效果。

周期交流电流 i(t) 在一个周期T 时间内在电阻R上消耗的电能为：

直流电流I在一个周期T 时间内在电阻R上消耗的电能为：

W₂=I²RT

按照有效值的定义，若W₁ = W₂，则

电流的有效值是交流电流在一个周期内的均方根值。

类似地，周期电压的有效值：

正弦电流、电压的有效值

设 i(t)=I_mcos(ωt+φ)

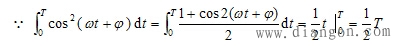
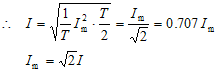　注意:只适用正弦量。

有效值的概念也适用于任何其他周期性的交流电压和电流。

问题与讨论：

若购得一台耐压为 300V 的电器，是否可用于 220V 的正弦交流线路上?

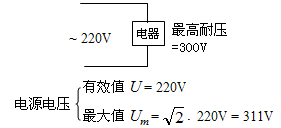
该电器最高耐压低于正弦交流电源电压的最大值，所以不能用！

2.频率与周期

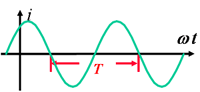
（1）周期 T：变化一周所需的时间，单位：s。

（2） 频率 f：每秒变化的次数，单位：Hz。

（3）角频率ω：是正弦量的相位(ωt + φ)随时间变化的角速度(每秒变化的弧度)。即

角频率ω的单位为rad/s，与正弦量的周期T和频率f间的关系为:

小常识：

（1）电网频率： 中国 50 Hz

　　　　　　　　美国 、日本 60 Hz

（2）有线通讯频率：300 - 5000 Hz

（3）无线通讯频率： 30 kHz - 3×10⁴ MHz

3.初相位与相位差

（1）相位角（或相位）：(ωt + φ)。

（2）初相位： t = 0 时的相位，或称为初相角。

初相角的绝对值一般小于180^ｏ

即规定： |φ|≤π (180°)

说明：初相角给出了观察正弦波的起点或参考点，常用于描述多个正弦波相互间的相位关系。

（3）相位差(phase difference) ：

两个同频率正弦量的相位角之差。

设:

相位差:

　　等于它们的初相角之差

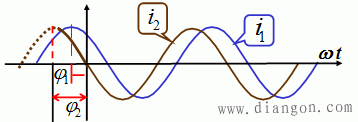
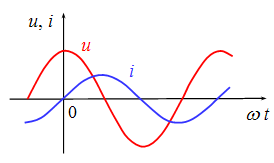
相位差:→i₂ 领先(超前)i₁

同频率正弦量的相位差等于它们的初相之差，与时间无关。

电路中采用“超前”和“滞后”来说明它们相位比较的结果。

同频率正弦量的相位差可通过观察波形确定，在同一周期内两个波形的极大值(或极小值)间的角度值(≤1800)，即为两者的相位差。超前者先达到极值点。

相位差与计时零点的选取、变动无关。

两种正弦信号的相位关系

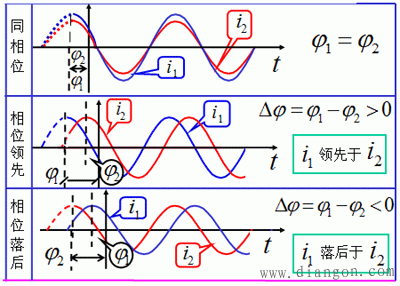
特殊相位关系：

△φ= 0，称ｕ和i同相：

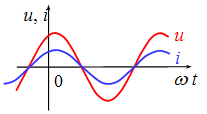
△ φ=± π (±180^o ) ， 称ｕ和i反相：

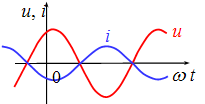
△φ=90°称ｕ和i正交。u领先i90° 或i落后u90°

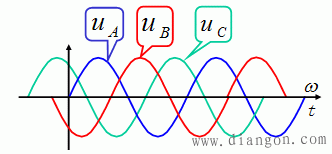
三相交流电路：三个电压初相位各差120°。

正弦量乘以常数，正弦量的微分，积分，同频率正弦量的代数和等运算，其结果仍为一个同频率的正弦量。

如：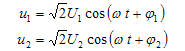

则：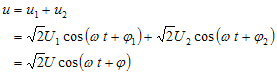

幅度、相位变化频率不变

结论:

因角频率（ω）不变，所以以下讨论同频率正弦量时，ω可不考虑，主要研究幅度与初相位的变化。