2.如果电路有多个激励且都是同一频率的正弦量,则根据线性电路的叠加性质,电路全部稳态响应都将是同一频率的正弦量。
处于稳定工作状态的正弦交流电路称为正弦稳态电路。
(1)电力工程中遇到的大多数问题都可以按正弦稳态电路分析处理。
(2)许多电气、电子设备的设计和性能指标也往往是按正弦稳态考虑的。
(3)电工技术中的非正弦周期函数可以分解为频率成整数倍的正弦函数的无穷级数。这类问题也可以应用正弦稳态方法处理。
相量法是分析求解正弦交流电路稳态响应的一种简便有效的工具。
3.旋转有向线段(旋转相量)
概念 :一个正弦量的瞬时值可以用一个旋转的有向线段在纵轴上的投影值来表示。
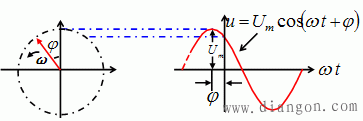
取有向线段(相量)
矢量长度 = Um
矢量与纵轴夹角 = 初相位φ
矢量以角速度 ω按逆时针方向旋转
4.正弦量的相量表示
复函数
![]()
![]()
若对F(t)取实部:
![]()
![]()
F(t)还可以写成
![]()
![]()
称![]() 为正弦量 i(t) 对应的相量。
为正弦量 i(t) 对应的相量。
![]()
![]()
正弦量的相量表示:
相量的模表示正弦量的有效值
相量的幅角表示正弦量的初相位
注意:
(1)正弦量的相量和它时域内的函数表达式是一一对应的关系,不是相等的关系。
只有正弦量才能用相量表示,非正弦量不可以。
(2)若已知正弦量时域表达式,可直接写出与之对应的相量。
![]()
(3)若已知正弦量的相量,须再知道其角频率才可写出与之对应的函数表达式。
![]()
相量的书写方式:
相量是一个复数,它在复平面上的图形称为---相量图
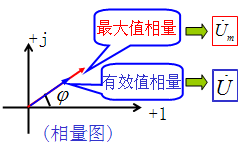
(1)描述正弦量的有向线段称为相量 (phasor )。若其用最大值相量表示,则用符号:![]() 。
。
(2)在实际应用中,更多采用有效值相量,则用符号:![]() 。
。
(3)相量符号![]() 包含有效值与相位信息。.
包含有效值与相位信息。.
5.相量表示法
相量图
同频率正弦量按大小和相位在复平面上画在一起构成的图形。
例1.
已知: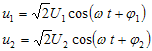
设 ![]()
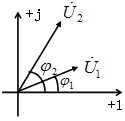
求:将 u1、u2 用相量图表示。

只有同频率的正弦量才能画在一张相量图上,不同频率不行。
