1.同频率正弦量相加减
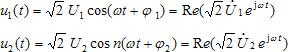
![]()
![]()
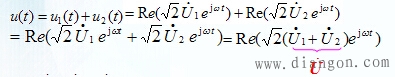
得:![]()
这实际上是一种变换思想,由时域变换到频域。
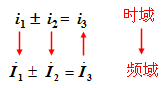
时域:在变量是时间函数条件下研究网络,以时间为自变量分析电路。
频域:在变量经过适当变换的条件下研究网络,以频率为自变量分析电路。
相量法:将正弦时间函数 “变换” 为相量后再进行分析, 属于频域分析。
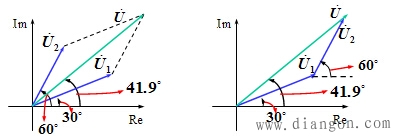
例2.
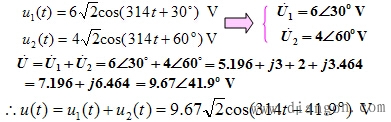
同频正弦量的加、减运算可借助相量图进行。相量图在正弦稳态分析中有重要作用,尤其适用于定性分析。
2.正弦量的微分,积分运算
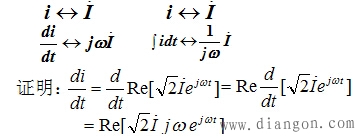
(1)正弦量的导数是一个同频率的正弦量,其相量等于原正弦量的相量乘以jω,即表示di/dt 的相量为: ![]()
该相量的模为ωI ,辐角则超前原相量π/2 。
(2)正弦量的积分结果为同频率的正弦量,其相量等于原正弦量的相量除以jω,即表示∫idt 的相量为: ![]()
该相量的模为 I /ω ,辐角则滞后原相量π/2。
