二端口的联结

一个复杂二端口网络可以看作是由若干简单的二端口按某种方式联接而成，这将使电路分析得到简化，因此讨论两端口的连接问题具有重要意义。
　　1. 两端口的级联 (链联)

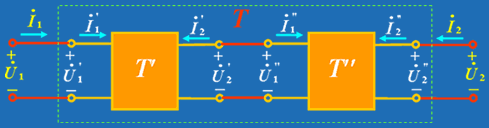图 1

　　图 1为两个两端口的级联，设两个两端口的 T 参数分别为：
　　　　　 　　　
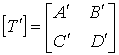
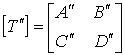
　　　则应有：　　
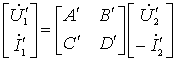
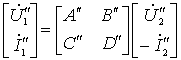
　　 级联后满足：　　　　　　
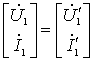
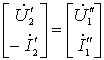
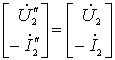
　　 综合以上各式得：
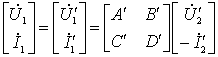
　　式中
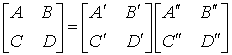
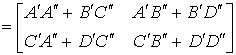
　　　　即：
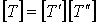
　　由此得出结论： 级联后所得复合二端口 T 参数矩阵等于级联的二端口 T 参数矩阵相乘。上述结论可推广到 n 个二端口级联的关系。
　　注意：
　　 1) 级联时 T 参数是矩阵相乘的关系，不是对应元素相乘。如：
　　　　　　
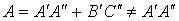
　　 2) 级联时各二端口的端口条件不会被破坏。

2. 两端口的并联 　　图 2为两个两端口的并联，并联采用 Y 参数比较方便。设两个两端口的 Y 参数分别为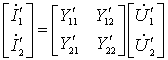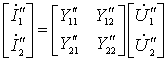： 　 　 并联后满足：
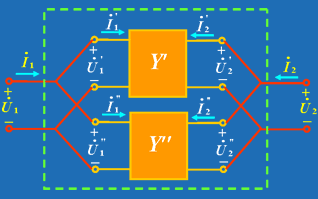	图 2

　　　　　　　　
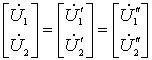
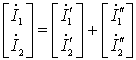
　　综合以上各式得：
　　　　
　　　　　　　
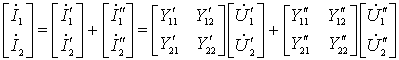
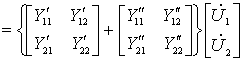
　　　　　　即：

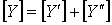
由此得出结论： 　　二端口并联所得复合二端口的Y 参数矩阵等于两个二端口 Y 参数矩阵相加。 注意： 　　1)两个二端口并联时，其端口条件可能被破坏此时上述关系式就不成立。 　　2)具有公共端的二端口(三端网络形成的二端口)如图3所示，将公共端并在一起将不会破坏端口条件。
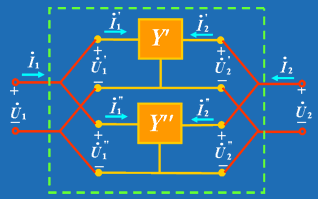	图 3

3)检查是否满足并联端口条件的方法如图 4所示，即在输入并联端与电压源相连接，Y'、Y” 的输出端各自短接，如两短接点之间的电压为零，则输出端并联后，输入端仍能满足端口条件。用类似的方法可以检查输出端是否满足端口条件。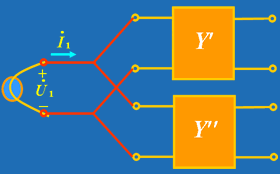
	图4

　　3. 两端口的串联

图 5为两个两端口的串联，串联采用 Z 参数比较方便。设两个两端口的 Z 参数分别为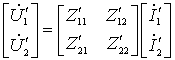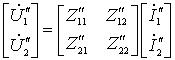： 　 　 　 　 并联后满足：
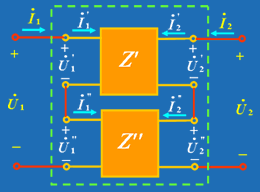	图 5

　　　　　　
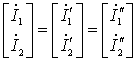
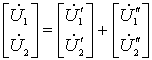
　　综合以上各式得：
　　　　

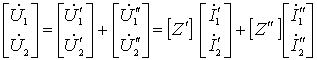
即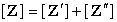： 　　 由此得出结论： 　　串联后复合二端口 Z 参数矩阵等于原二端口 Z 参数矩阵相加。可推广到 n 端口串联。 　　注意： 　　1)串联后端口条件可能被破坏。需检查端口条件。 　　2)具有公共端的二端口，将公共端串联时将不会破坏端口条件，如图 6所示。
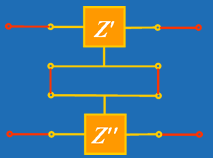	图 6

3) 检查是否满足串联端口条件的方法如图7所示，即在输入串联端与电流源相连接，a'与 b 间的电压为零，则输出端串联后，输入端仍能满足端口条件。用类似的方法可以检查输出端是否满足端口条件。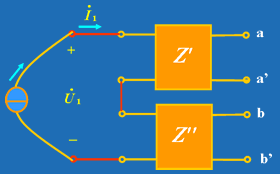
	图 7