在线性电路中, 线性元件的特点是其参数不随电压或电流而变化。如果电路元件的参数随着电压或电流而变化, 即电路元件的参数与电压或电流有关, 就称为非线性元件, 含有非线性元件的电路称为非线性电路。
实际电路元件的参数总是或多或少地随着电压或电流而变化, 所以严格说来, 一切实际 电路都是非线性电路。但在工程计算中,可以对非线性程度比较弱的电路元件做为线性元件来处理, 从而简化电路分析。而对许多本质因素具有非线性特性的元件,如果忽略其非线性特性就将导致计算结果与实际量值相差太大而无意义。因此,分析研究非线性电路具有重要的工程物理意义。
2.非线性电阻
线性电阻元件的伏安特性可用欧姆定律来表示, 即
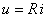 , 在
, 在 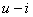 平面上它是通过坐标原点的一条直线。非线性电阻元件的伏安关系不满足欧姆定律, 而是遵循某种特定的非线性函数关系。非线性电阻在电路中符号如图 17.1(a)所示。
平面上它是通过坐标原点的一条直线。非线性电阻元件的伏安关系不满足欧姆定律, 而是遵循某种特定的非线性函数关系。非线性电阻在电路中符号如图 17.1(a)所示。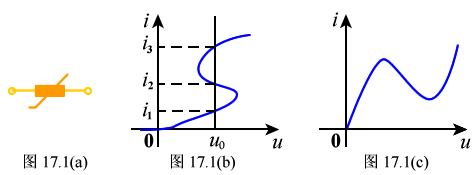
(1)电流控制型电阻:非线性电阻元件两端电压是其电流的单值函数, 它的伏安特性可用下列函数关系表示:
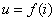
其典型的伏安特性如图17.1(b)所示, 从其特性曲线上可以看到: 对于同一电压值,与之对应的电流可能是多值的。如
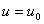 时, 就有
时, 就有 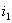 、
、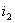 和
和 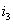 3个不同的值与之对应。而对于每一个电流值
3个不同的值与之对应。而对于每一个电流值 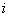 , 有且只有一个电压值
, 有且只有一个电压值 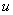 与之对应。
与之对应。(2)电压控制型电阻:通过非线性电阻元件中的电流是其两端电压的单值函数,其伏安特性可用下列函数关系表示:
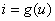
其典型的伏安特性如图17.1(c)所示,从其特性曲线上可以看到: 对于同一电流值, 与之对应的电压可能是多值的。但是对于每一个电压值
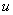 , 有且只有一个电流值
, 有且只有一个电流值 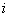 与之对应。隧道二极管就具有这样的伏安特性。
(3)单调型非线性电阻:非线性电阻元件的伏安特性是单调增长或单调下降的,它同时是电流控制又是电压控制的。这类电阻以
与之对应。隧道二极管就具有这样的伏安特性。
(3)单调型非线性电阻:非线性电阻元件的伏安特性是单调增长或单调下降的,它同时是电流控制又是电压控制的。这类电阻以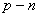 结二极管最为典型, 其伏安特性用下式表示
结二极管最为典型, 其伏安特性用下式表示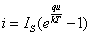
式中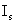 为一常数,称为反向饱和电流, 为一常数,称为反向饱和电流, 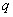 是电子的电荷( 是电子的电荷(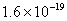 库), 库), 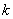 是波尔兹曼常数 是波尔兹曼常数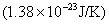 , , 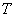 为热力学温度。在 为热力学温度。在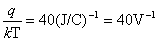 因此 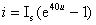 从式 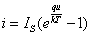 可求得 可求得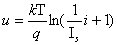 换句话说,电压可用电流的单值函数来表示。它的伏安特性曲线如图17.2 所示。 |
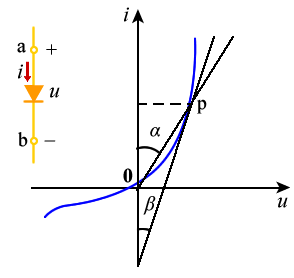 |
图 17.2  结二极管的伏安特性 结二极管的伏安特性 |
非线性电阻元件在某一工作状态下(如图17.2中
 点)的静态电阻
点)的静态电阻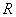 等于该点的电压值
等于该点的电压值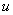 与电流值
与电流值 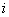 之比, 即
之比, 即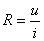
显然
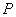 点的静态电阻正比于
点的静态电阻正比于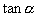 。
。 非线性电阻元件在某一工作状态下(如图17.2中
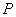 点)的动态电阻
点)的动态电阻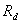 等于该点的电压
等于该点的电压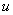 对电流
对电流 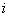 的导数值, 即
的导数值, 即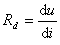
显然
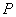 点的动态电阻正比于
点的动态电阻正比于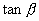 。
。这里特别要说明的是,当非线性电阻伏安特性某一点处的动态电阻为负值时,称非线线性电阻在该点具有“负电阻”的性质。
(6)非线性电阻的串联和并联
当非线性电阻元件串联或并联时,只有所有非线性电阻元件的控制类型相同,才有可能得出其等效电阻伏安特性的解析表达式。对于下图所示两个非线性电阻的串联电路,设两个非线性电阻的伏安特性分别为
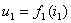 ,
, 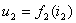 , 用
, 用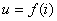 表示图17.3(a)所示两个非线性电阻串联电路的一端口伏安特性。根据
表示图17.3(a)所示两个非线性电阻串联电路的一端口伏安特性。根据 和
和 ,得:
,得: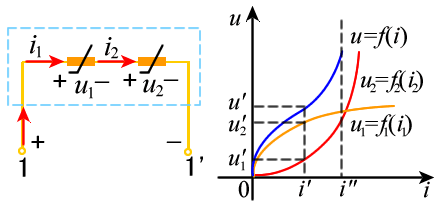
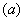
图 17.3 非线性电阻的串联
又有
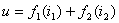
因此对所有
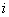 , 则有
, 则有 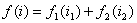
因此两个电流控制的非线性电阻串联组合的等效电阻还是一个电流控制的非线性电阻。
也可以用图解的方法来分析非线性电阻的串联电路。图17.3(b)说明了这种分析方法,即在同一电流值下将
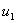 和
和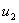 相加可得出
相加可得出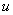 。例如,当
。例如,当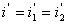 时,有
时,有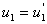 ,
,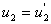 ,而
,而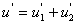 。取不同的
。取不同的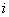 值,可逐点求出其等效伏安特性
值,可逐点求出其等效伏安特性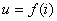 , 如图17.3(b)。
, 如图17.3(b)。如果这两个非线性电阻中有一个是电压控制型, 在电流值的某范围内电压是多值的,很难写出等效伏安特性
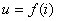 的解析式。可以用图解的方法求其等效伏安特性。
的解析式。可以用图解的方法求其等效伏安特性。图17.4(a)所示电路由线性电阻
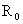 和直流电压源
和直流电压源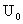 及一个非线性电阻
及一个非线性电阻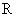 组成。线性电阻
组成。线性电阻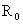 和电压源
和电压源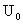 的串联组合可以是一个线性一端口的戴维宁等效电路。设非线性电阻的伏安特性如图17.4(b)所示。这里介绍另一种图解法, 称为“曲线相交法”。
的串联组合可以是一个线性一端口的戴维宁等效电路。设非线性电阻的伏安特性如图17.4(b)所示。这里介绍另一种图解法, 称为“曲线相交法”。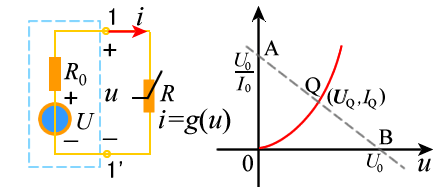
(a) (b)
图 17.4 静态工作点
对此电路用
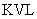 , 可得下列方程
, 可得下列方程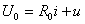
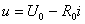
此方程可以看作是图17.4(a)虚线方框所示一端口的伏安特性。它在
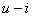 平面上是一条如图17.4(b)中的直线
平面上是一条如图17.4(b)中的直线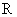 的伏安特性可表示为
的伏安特性可表示为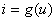
直线
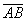 与此伏安特性的交点
与此伏安特性的交点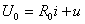 和
和 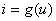 ,所以有:
,所以有: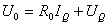
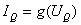
交点
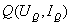 称为电路的静态工作点,它就是图17.4(a)所示电路的解。在电子电路中直流电压源通常表示偏置电压,
称为电路的静态工作点,它就是图17.4(a)所示电路的解。在电子电路中直流电压源通常表示偏置电压,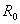 表示负载,故直线
表示负载,故直线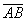 通常称为负载线。
通常称为负载线。 图17.5为两个非线性电阻的并联电路。按
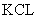 和
和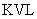 有
有
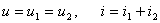 设两个非线性电阻均为电压控制型的,其伏安特性分别表示为 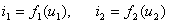 由此并联电路组成的一端口伏安特性用 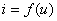 来表示。利用以上关系,可得 来表示。利用以上关系,可得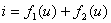 |
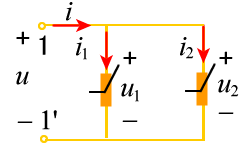 |
| 图17.5 非线性电阻的并联 |
用图解法来分析非线性电阻的并联电路时,把在同一电压值下的各并联非线性电阻的电流值相加,即可得到所需要的驱动点特性。
