随时间按正弦规律变化的电压和电流分别称为正弦电压和正弦电流，一般可用正弦时间函数式表示如下 ( 此处以电压为例 )
（ 1 ）
同 — 正弦电压也可用余弦函数表示为
式中 
本文中，一般均采用前 — 种表示法。
式 (1) 中， 
为正弦电压的幅值即极大值； 
为正弦函数的辐角〔argument) ，称为瞬时相角，简称相角 (phase) 或相 (phase), 它是随时间而变化的； 
为t=0 时的瞬时相角，称为初相角．简称初相 (initial phase) 。瞬时相角决定着正弦函数随时间t 变化的进程，而初相则表示在初始时刻正弦函数的辐角。设正弦电压随时间变化的周期(period) 为 T, 频率为
，则式 (6—1—1) 中，当时间 t 从零增加至 T 时，对应的辐角应增加 2 π。 换言之， 
故 
（ 2 ）
表示每经过单位时间，瞬时相角所增加的角度，称为角频率，在国际单位制中，角频率的单位为弧度每秒 ( 符号为 rad/s) 。它与正弦量的频率成正比。
任一正弦量，其幅值、初相及角频率 ( 或频率 ) 确定以后，该正弦量就被完全地确定下来。故幅值、初相及角频率称为正弦量的三要素。
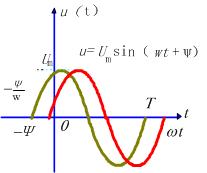
图 1 正弦交流电压波形
正弦电压和电流也可用波形图表示。图 6—1—1 绘出了两个频率及幅值相同而初相不同的正弦电压 
和 
的波形。图中的横坐标分别以时间 t 及角度 
t 为自变量标出。
由图可知，两个正弦被之间存在着相角差 (phase difference) 
，并且 
的相角超前于 
的相角，或者说 
的相角滞后于 
的相角。 一般设两个同频率的正弦量 
和 
分别为
它们之间的相位差
即等于二者的初相之差。 
是 
超前于 
的相角；反之， 
则是 
超前于 
的相角。如果， 
，即 
则称 
与 
同相 (in phase) ；反之，如果 
，则称 
与 
反相 (opposite phase) 。
在正弦电流电路的分析、汁算和实际应用中，通常采用有效值表示正弦电压、电流的大小 ( 而不是用幅值 ) 。下面以电流为例介绍有效值的概念。
首先研究周期电流的有效值。对于任何一个随时间按一定周期规律变化的 电流，在实际应用中，常常没有必要表示出它在每一瞬时的值，而希望定义一个 能够反映周期电流平均作功能力的量，即所谓的有效值。
周期电流的有效值定义为与周期电流的平均作功能力等效的直流电流的 值。设周期电流为 
，当其通过电阻 R 时，该电阻在一个周期 (T) 的时间内吸收的平均功率为
而同一电阻 R 通以直流电流 
时，该电阻吸收的功率为
根据前面对有效值的定义，令 
即 
这时的直流电流之值 
，即为周期电流的有效值，用 I 表示，则
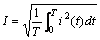（ 3 ）
式 （ 3 ）为周期电流的有效值的计算公式。由此式可知，周期电流的有效值等于它的瞬时值 ( 时间函数式 ) 的平方在一周期内的平均值的平方根。按其计算步骤，有效值又可称为均方根值 (root-mean-square value) 。
为了计算正弦电流的有效值，将正弦电流的时间函数式
代人式 (3) ，得
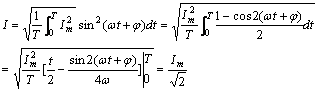（ 4 ）
上式表明，正弦电流的有效值等于其幅值除以 
。以上关于周期电流、正弦电流有效值的计算公式，即式 (3) 和式 (4) ，也分别适用于随时间作周期性变化和正弦变化的电压以及其它物理量的有效值计算。 在工程上，谈到正弦电流、电压等量的值而无特殊声明时，一般均指有效值。