当动态电路中所有储能元件都没有原始储能 ( 电容元件的电压为 0 ,电感元件的电流为 0) 时,换路后仅由输入激励(独立源)产生的响应称为零状态响
应。
RC电路的零状态响应
所谓RC 电路的零状态,是指换路前电容元件未储有能量,在此条件下,由独立源激励所产生的电路响应,称为零状态响应。分析 RC 电路的零状态响应,实际上是分析电容元件的充电过程。 如图1 所示RC 电路,![]() 时刻,开关断开,电路处于零初始状态;
时刻,开关断开,电路处于零初始状态; ![]() 时开关闭合。其物理过程为:开关闭合瞬间,电容电压不能跃变,电容相当于短路,此时
时开关闭合。其物理过程为:开关闭合瞬间,电容电压不能跃变,电容相当于短路,此时 ![]() ,充电电流
,充电电流 ![]() ,为最大;随着电源对电容充电,
,为最大;随着电源对电容充电, ![]() 增大,电流逐渐减小;当
增大,电流逐渐减小;当 ![]() 时,
时, ![]() ,
, ![]() ,充电过程结束,电路进入另一种稳态。
,充电过程结束,电路进入另一种稳态。
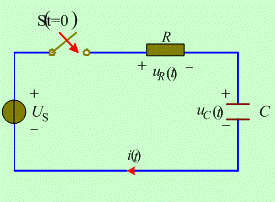
图1 RC电路的零状态响应
当 ![]() 时,由 KVL定律可得 :
时,由 KVL定律可得 : ![]()
把 ![]() ,
, ![]() 代入得
代入得
![]() ( 1 )
( 1 )
此方程为一阶线性非齐次微分方程,初始条件为 ![]() 。方程的解由非齐次微分方程的特解
。方程的解由非齐次微分方程的特解 ![]() 和对应齐次微分方程的通解
和对应齐次微分方程的通解 ![]() 组成,即
组成,即
![]() ( 2 )
( 2 )
不难求得其特解为: ![]() (3 )
(3 )
而对应的齐次方程 ![]() 的通解为:
的通解为:
![]() ( 4 )
( 4 )
其中, A 为待定常数 , ![]() 为 RC 电路时间常数。故,
为 RC 电路时间常数。故,
![]() (5 )
(5 )
代入初始条件 ![]() ,可得
,可得 ![]() 。
。
所以 ![]() ( 6 )
( 6 )
电路中的电流为: ![]() ( 7 )
( 7 )
![]() 和
和 ![]() 的零状态响应波形如图 2 所示。可见:在直流电压源激励下,电容电压不能突变,须经历一个动态的充电过程,充电速度取决于时间常数
的零状态响应波形如图 2 所示。可见:在直流电压源激励下,电容电压不能突变,须经历一个动态的充电过程,充电速度取决于时间常数 ![]() ,当电容电压达到电源电压
,当电容电压达到电源电压 ![]() 时充电结束,电路进入稳态;电容电流
时充电结束,电路进入稳态;电容电流 ![]() 换路瞬间发生突变,随充电过程的进行逐渐下降,下降速度取决于时间常数
换路瞬间发生突变,随充电过程的进行逐渐下降,下降速度取决于时间常数 ![]() ,充电结束后,电流为零,电路进入稳态。充电过程中电容元件获得的能量
,充电结束后,电流为零,电路进入稳态。充电过程中电容元件获得的能量![]() 以电场能量形式储存。
以电场能量形式储存。
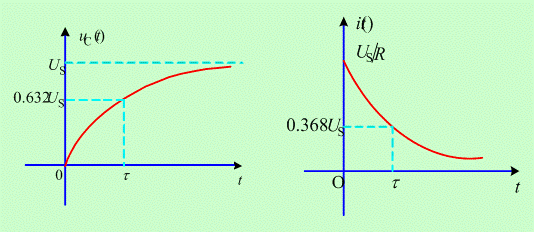
图 2 ![]() 和
和 ![]() 的零状态响应波形
的零状态响应波形
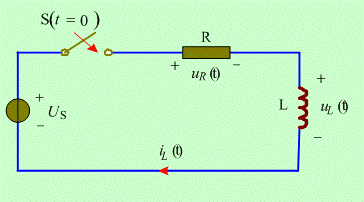
图 3 RL电路的零状态响应
RL电路的零状态响应
如图 3 所示,在换路前 ( t<0) 开关处于断开状态,电感元件 L 处于零初始状态,即 ![]() 。 t=0时刻开关闭合瞬间,电路即与一恒定电压为
。 t=0时刻开关闭合瞬间,电路即与一恒定电压为 ![]() 的电压源接通,此时相当于接入一个阶跃电压。
的电压源接通,此时相当于接入一个阶跃电压。
![]() 时 , 根据 KVL 基尔霍夫电压定律 :
时 , 根据 KVL 基尔霍夫电压定律 :
![]()
把 ![]() ,
, ![]() 代入并整理得
代入并整理得
![]() ( 8 )
( 8 )
这也是一个一阶非齐次微分方程,其初始条件为: ![]() .
.
与 RC 电路相似,电流 ![]() 的解可分为微分方程的特解
的解可分为微分方程的特解 ![]() 和通解
和通解 ![]() 两部分。容易求得特解
两部分。容易求得特解 ![]() ,同解可表示为
,同解可表示为 ![]() 。故
。故
![]()
代入初始条件 ![]() ,得
,得 ![]() 。所以
。所以
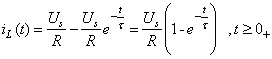 (8 )
(8 )
电感两端的电压为
![]() ( 9 )
( 9 )
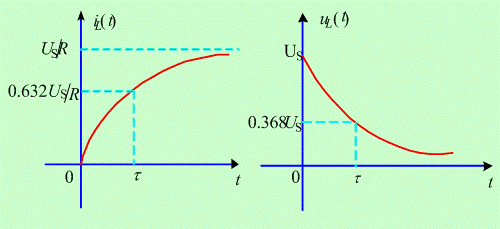
![]() 和
和 ![]() 的零状态响应随时间的变化规律如图 4 所示。
的零状态响应随时间的变化规律如图 4 所示。
对比图 2 与图 4 可见,一阶 RC 电路与一阶 RL 电路有强烈的对偶性: 在直流电压源激励下,电感电流 ![]() 不能突变,须经历一个动态充电过程,变化速度取决于时间常数
不能突变,须经历一个动态充电过程,变化速度取决于时间常数 ![]() ,当电感电流达到
,当电感电流达到 ![]() 时电路进入稳态;电感电压
时电路进入稳态;电感电压 ![]() 在换路瞬间发生突变,随充电过程的进行逐渐下降,下降速度取决于时间常数
在换路瞬间发生突变,随充电过程的进行逐渐下降,下降速度取决于时间常数 ![]() ,充电结束后,电压为零,电路进入稳态。充电过程中电感元件获得的能量
,充电结束后,电压为零,电路进入稳态。充电过程中电感元件获得的能量 ![]() 以磁场能量形式储存。
以磁场能量形式储存。
(a) ( b )
图 4 ![]() 和
和 ![]() 的零状态响应
的零状态响应