在数学上,二阶电路的输入 - 输出方程表现为二阶线性微分方程;在物理结构上,二阶电路包含两个独立的动态元件,可以是一个电感与一个电容、两个电感或两个电容。需要注意的是,电路是否为二阶电路不能仅根据包含动态元件的数量来判断。若电路中包含一个电感与一个电容,则电路必为二阶电路;若电路中包含多个电容或多个电感,则需根据相互之间连接关系来判断,若经串、并联后可合并为一个电容或电感,则电路为一阶电路;若经串、并联简化为最简形式后仍存在两个独立的电容或电感,则电路为二阶电路;若独立电容或电感数大于两个,则电路为高阶电路。
在一阶电路中,仅包含一个独立的动态元件,它可以吸收独立源提供的能量加以储存,它储存的能量也可以通过电阻回路进行释放。在二阶电路中,由于存在两个独立的动态元件,二者均可以一定的形式储存能量和释放能量,但二者在动态过渡过程中存在能量交互的现象,即两个动态元件交互地释放和吸收能量,在响应信号波形上体现为一定的振荡现象。二阶电路的能量交互现象所遵循的规律取决于具体电路结构和元件参数的配置。
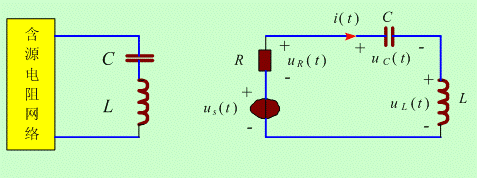
(a) 一般 RLC 串联电路 (b) 戴维宁等效后电路
图1 RLC 串联电路的一般模型
包含一个电容元件与一个电感元件的 RLC 串联电路和 RLC 并联电路是最基本的二阶电路,也是我们的学习重点。任意 RLC 串联电路由一对串联的电感、电容与一个含源电阻网络组成,其电路模型如图1 (a) 所示。将含源电阻网络经戴维宁等效,可以得到 RLC 串联电路的通用模型,如图1(b) 所示。而任意 RLC 并联电路由一对并联的电感、电容与一个含源电阻网络组成,其电路模型如图2 (a) 所示。将含源电阻网络经诺顿等效,可以得到 RLC 并联电路的通用模型,如图2(b) 所示。

(a) 一般 RLC 并联电路 (b) 诺顿等效后电路模型
图2 RLC 并联电路的一般模型
对图1 (b) 所示 RLC 串联电路,根据 KVL 列出电路方程
![]() ( 1 )
( 1 )
由于 ![]() ,
,
故: ![]() ,
, ![]() 。
。
将上述关系代入 (1 ) 并整理,得到 RLC 串联电路的输入 - 输出方程
![]() ( 2 )
( 2 )
对图 2 (b) 所示 RLC 并联电路,根据 KCL 列出电路方程
![]() ( 3 )
( 3 )
由于 ![]() ,
,
故
![]() ,
, ![]() 。
。
将上述关系代入 ( 3 ) 并整理,得到 RLC 并联电路的输入 - 输出方程
![]() (4 )
(4 )
在 (2 ) 式和 (4) 式二阶微分方程的基础上,我们根据初始条件和激励信号即可求解 RLC 串联电路和 RLC 并联电路的零输入响应和零状态响应。
