适用于直流激励一阶电路的三要素法
我们仍以简单一阶 RC 电路为出发点。 图1 所示 RC 电路的全响应结果如下:
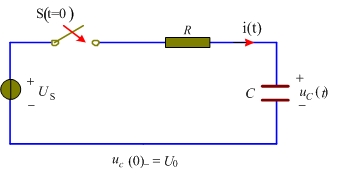
图 1 一阶RC电路图
![]() ( 1 )
( 1 )
![]() ( 2 )
( 2 )
由 图1 容易知道,电容电压 ![]() 的初值为
的初值为 ![]() ,电容电压的终值为
,电容电压的终值为 ![]() ;而电流
;而电流 ![]() 的初值为
的初值为 ![]() ,电流
,电流 ![]() 的终值为
的终值为 ![]() 。
。
观察式 ( 1 ) 、式 (2) 可见,一阶电路中任意电路变量的全响应具有如下的统一形式:
![]() ( 3 )
( 3 )
可见,为求解一阶电路中任一电路变量的全响应,我们仅须知道 三个要素 :电路变量的 初值 ![]() 、电路变量的 终值
、电路变量的 终值 ![]() 以及一阶电路的 时间常数
以及一阶电路的 时间常数 ![]() 。我们称式 ( 6-5-3 ) 为一阶电路分析的 三要素法 。三要素法同样适用于一阶 RL 电路,但是二阶以上动态电路不可采用此法。
。我们称式 ( 6-5-3 ) 为一阶电路分析的 三要素法 。三要素法同样适用于一阶 RL 电路,但是二阶以上动态电路不可采用此法。
推广的三要素法
在前面分析一阶电路时,我们采用的独立源具有共同的特点,即所有独立源均为直流(直流电压源或直流电流源)。对于直流激励电路,换路前电路变量为稳定的直流量,换路后经历一个动态过程,电路变量过渡到另外一个稳定的直流量。我们容易根据电路的原始状态和电路结构确定电路变量的 初值f(0+)、电路变量的 终值 f(∞)以及一阶电路的 时间常数 ![]() 。如果电路中激励源不是直流,而是符合一定变化规律的交流量(如正弦交流信号),则换路后电路经历一个动态过程再次进入稳态,此时的稳态响应不再是直流形式,而依赖于激励源的信号形式(如正弦交流信号)。此时,我们无法确定电路变量的 终值f(∞),故无法采用式 ( 3 ) “三要素法 ” 确定一阶电路全响应。对于这类一阶电路,我们可以采用推广的三要素法:
。如果电路中激励源不是直流,而是符合一定变化规律的交流量(如正弦交流信号),则换路后电路经历一个动态过程再次进入稳态,此时的稳态响应不再是直流形式,而依赖于激励源的信号形式(如正弦交流信号)。此时,我们无法确定电路变量的 终值f(∞),故无法采用式 ( 3 ) “三要素法 ” 确定一阶电路全响应。对于这类一阶电路,我们可以采用推广的三要素法:
![]() 〔 4 )
〔 4 )
式中, ![]() 为全响应的 初值 、
为全响应的 初值 、 ![]() 为电路的 稳态响应 、τ为电路的 时间常数 ,称为一阶线性电路全响应的 三要素 ,
为电路的 稳态响应 、τ为电路的 时间常数 ,称为一阶线性电路全响应的 三要素 , ![]() 为全响应稳态解的初始值。
为全响应稳态解的初始值。
“三要素”的计算与应用
利用三要素法分析一阶电路的全响应时,必须首先计算出电路变量的 初值![]() 、电路变量的 终值
、电路变量的 终值 ![]() 以及一阶电路的 时间常数
以及一阶电路的 时间常数 ![]() 。。假设激
。。假设激
励源为直流电压源或电流源。
• 初值 f(0+) 的计算
换路前,一般认为电路已进入稳态。根据电路结构以及元件属性,我们不难确定动态元件的原始状态(电容元件的电压 ![]() 或电感元件的电流
或电感元件的电流 ![]() )。在有限激励的作用下,电容元件的电压或电感元件的电流不会发生突变。因此,在
)。在有限激励的作用下,电容元件的电压或电感元件的电流不会发生突变。因此,在 ![]() 时刻,电容元件的电压
时刻,电容元件的电压 ![]() 或电感元件的电流
或电感元件的电流 ![]() 维持原始状态不变。我们可以用一个电压源
维持原始状态不变。我们可以用一个电压源 ![]() 取代电容元件,或用一个电流源
取代电容元件,或用一个电流源 ![]() 取代电感元件。此时,电路被转换成电阻电路,借助于电阻电路的支路分析法、回路分析法、结点分析法、戴维宁定理等即可计算出响应信号的初值
取代电感元件。此时,电路被转换成电阻电路,借助于电阻电路的支路分析法、回路分析法、结点分析法、戴维宁定理等即可计算出响应信号的初值 ![]() 。
。
• 终值 f(∞)的计算
换路后,动态电路经过一个过渡过程,再次进入稳态。在直流激励情况下, t=∞时,电容电压和电感电流维持某个不变的取值。电容元件电流为 0 ,可以用开路元件取代,电感元件电压为零,可以用短路元件取代。与初值计算相似,电路被转换成电阻电路,借助于电阻电路的分析方法即可计算出响应信号的终值 f(∞)。
• 时间常数 τ的计算
实际的一阶电路可能元件数量较大,结构较复杂,电路中包含多个电阻元件、独立源、受控源和多个电容或电感。若电路满足一阶电路的条件,则其中的电容元件或电感元件之间必有强烈的相关性,表现在电路连接上为串联、并联或混联关系。此时,换路后的电路模型可以看作由为某个电容网络或电感网络与一个含源电阻网络相连组成,如图2 ( a )所示。对电路中电容网络或电感网络进行串、并联计算,得到一个等效电容 C eq 或一个等效电感Leq ,将含源电阻网络进行诺顿等效或戴维宁等效,得到图2 ( b )所示等效一阶电路。则一阶电路的时间常数τ 可计算如下:
![]() 或
或 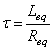 〔5 )
〔5 )
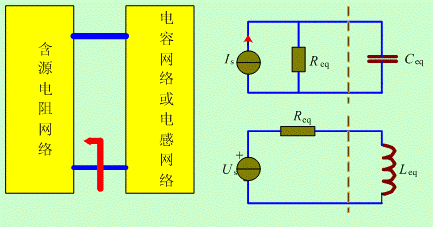
( a )电路模型分解 ( b )等效电路
图2 一阶电路的电路模型分解与等效
