图示电路开关原是断开的,电感电流![]() 。
。![]() 时开关接通。
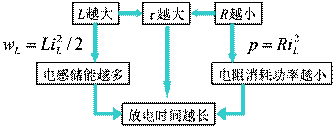
时开关接通。![]() 时就得到图(b)示RL电路。其KVL方程为
时就得到图(b)示RL电路。其KVL方程为
![]()
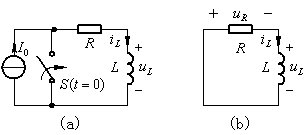
RL电路的零输入响应
根据换路定律 ![]()
1)方程解
一阶齐次微分方程,其特征方程和特征根分别为![]() ;
;![]()
通解 ![]()
式中 ![]()
称为RL电路的时间常数,当电感单位为H,电阻单位为![]() 时,
时,![]() 的单位也是s。
的单位也是s。
由初始条件,确定通解积分常数A:![]()
代入通解得 ![]()
![]()
根据电阻或电感的元件方程求得![]()

![]() 及
及![]() 的变化曲线
的变化曲线
零输入响应![]() 和
和![]() 按同一指数规律衰减至零。
按同一指数规律衰减至零。![]() 是连续变化的,而电感电压
是连续变化的,而电感电压![]() 则从
则从![]() 时的零值跃变到
时的零值跃变到![]() 时的
时的![]() 。若电阻R很大,则在换路时电感两端会出现很高的瞬间电压。
。若电阻R很大,则在换路时电感两端会出现很高的瞬间电压。
2)对时间常数的理解
例1.图示电路,已知![]() ,
,![]() 。
。![]() 时电路处于直流稳态。
时电路处于直流稳态。![]() 时开关断开。求
时开关断开。求![]() 时的电流
时的电流![]() 及开关两端电压
及开关两端电压![]() 。
。
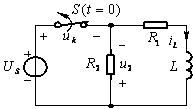
解:先计算![]() 。换路后
。换路后![]() 的电路与图10.7(b)所示RL电路相同,可直接引用其分析结果。
的电路与图10.7(b)所示RL电路相同,可直接引用其分析结果。![]() 的初始值及时间常数分别为
的初始值及时间常数分别为
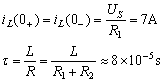
RL零输入通解表达式得 ![]()
再由KVL求得 ![]()
![]() 时,
时, ![]()
可见,在断开含电感的电路时,开关可能承受很高的电压。
例2.图示电路中 C 为高压电容器,且已充电完毕,uC (0-)=10kV。设 t =0 时,开关由端子1打到端子2,15分钟后,uC 降低为 3.2kV,问
(1) 再经过15分钟后电容电压降为多少?
(2) 如果电容C=15μF,R=?
(3) 需要多长时间电容电压可降至30V以下?
(4) 若 C 不变,R 变为0.2Ω,电容最大放电电流是多少?
若认为 t=5τ时放电完毕,那么放电的平均功率是多少?
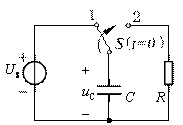
解:由已知为RC零输入响应
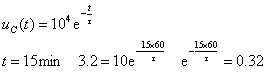
(1) ![]()
(2) ![]() ,
,![]()
(3) ![]()
(4) ![]() ;
;![]()
![]() ;
;![]()
![]()
