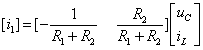1.状态变量与状态方程
在对一阶和二阶电路的分析中已经获知：如果确定了
与
在
时的初始值，又已知
时的外施激励，那么动态电路在
时的响应也就完全确定了。
状态变量 能完整地、确定地描述动态电路时域行为的最少变量，是一组独立的动态变量，如 uC和iL。
状态方程 由电路的状态变量及其一阶导数组成的一阶微分方程组。
2.状态方程列写
(1) 对联接一个电容的节点列KCL方程。
(2) 对包含一个电感的回路列KVL方程。
(3) 为消去上述方程中的非状态变量，用电压源
和电流源
分别置换电容和电感。由此电阻电路求出待消去的非状态变量。
(4) 消去非状态变量，整理成标准形式的状态方程。
式中，
称为状态变量列向量或状态向量。
表示状态变量的一阶导数列向量。
称为输入列向量。A是
方阵，n为状态变量个数。B是
矩阵，m是外加独立电源个数。A与B均由电路的结构和参数决定。
3.输出方程
将感兴趣的输出变量表示为状态变量和输入激励之间的关系写成矩阵形式的方程。
例1.列出图 (a)所示电路的状态方程的标准形式，并写出以
为输出变量的输出方程。
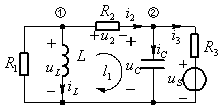
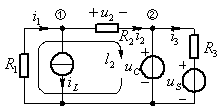
(a) (b)
解：对联接电容的节点②列KCL方程：
(1)
对包含电感的回路
列KVL方程：
(2)
为消去非状态变量
、
和
，分别用电压源和电流源置换电容与电感，得图10.49(b)所示电路。由该图得
(3)
(4)
对回路
列KVL方程：
解得
(5)
(6)
将式(3)、(5)代入式(1)，将式(6)代入式(2)，经整理得状态方程
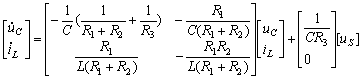(7)
将式(5)代入式(4)，经整理得输出方程
