设电路在![]() 时换路,确定各种电路变量初始值的方法。
时换路,确定各种电路变量初始值的方法。
1.电容电压![]() 初始值的确定
初始值的确定
设在线性电容![]() 上电压
上电压![]() 和电流
和电流![]() 参考方向相同,则有
参考方向相同,则有
![]()
电容电荷的初始值可表示为
![]()
式中右端第一项为![]() 的电荷
的电荷![]() , 故
, 故
![]()
若在![]() 瞬间电容电流
瞬间电容电流![]() 有界,则上式积分项必为零,于是得到
有界,则上式积分项必为零,于是得到
![]() 和
和 ![]() (10.3)
(10.3)
式中,![]() 和
和![]() 表示换路前瞬间电容电压和电荷。
表示换路前瞬间电容电压和电荷。
综上若换路瞬间![]() 有界,则
有界,则![]() 和
和![]() 在
在![]() 时是连续变化的或称渐变。
时是连续变化的或称渐变。
2.电感电流![]() 初始值的确定
初始值的确定
应用对偶原理由式(10.3)可直接写出电感电流和磁链的初始值与原始值的关系:
![]() 和
和 ![]() (10.4)
(10.4)
即若在换路瞬间电感电压![]() 有界,电感电流
有界,电感电流![]() 和磁链
和磁链![]() 在
在![]() 时是连续的。
时是连续的。
3.换路定律
式(10.3)和(10.4)及其成立的条件所表示的规律称为换路定律。 式中各原始值![]() 、
、![]() 和
和![]() 、
、![]() 是根据换路之前的电路算出的,然后根据换路定律便可求出初始值
是根据换路之前的电路算出的,然后根据换路定律便可求出初始值![]() 、
、![]() 、
、![]() 、
、![]() 。
。
因储能
![]() 和
和 ![]()
吸收或发出功率
![]() 和
和 ![]()
在实际电路中,功率![]() 和
和![]() 是有界的,故
是有界的,故![]() 和
和![]() 以及相关的
以及相关的![]() 、
、![]() 和
和![]() 、
、![]() 都是连续变化的,所以
都是连续变化的,所以![]() 、
、![]() 和
和![]() 、
、![]() 在换路瞬间服从换路定律。除
在换路瞬间服从换路定律。除![]() 和
和![]() 之外的各元件电压电流均与元件储能无关,在换路瞬间是可以跃变的。
之外的各元件电压电流均与元件储能无关,在换路瞬间是可以跃变的。
4.![]() 、
、![]() 之外电压电流初始值确定
之外电压电流初始值确定
![]() 和
和![]() 根据换路定律来确定,求其它电压、电流初始值
根据换路定律来确定,求其它电压、电流初始值![]() 和
和![]() 则须根据电路变量的结构约束和元件约束,即在
则须根据电路变量的结构约束和元件约束,即在![]() 瞬间有:
瞬间有:
KCL ![]()
KVL ![]()
电阻 ![]() 或
或![]()
电容元件 ![]() → 电容相当于电压源
→ 电容相当于电压源
电感元件 ![]() → 电感相当于电流源
→ 电感相当于电流源
![]() 瞬间,可用电压源和电流源来置换电容和电感。于是电路成为电阻电路,可用分析直流电路的各种方法来求解。
瞬间,可用电压源和电流源来置换电容和电感。于是电路成为电阻电路,可用分析直流电路的各种方法来求解。
| 元件 | 换路中 | 换路后 | 稳态/DC |
L | 开路 |
| 短路 |
C | 短路 |
| 开路 |
例1.图(a)所示电路,在![]() 时处于稳态,
时处于稳态,![]() 时开关接通。求初始值
时开关接通。求初始值![]() 、
、![]() 、
、![]() 、
、![]() 及
及![]() 。
。

解:开关在接通之前,电路是直流稳态,电容相当于开路,电感相当于短路。于是求得
![]() ;
;![]()
由换路定律得
![]()
![]() 时的等效电路列节点电压方程
时的等效电路列节点电压方程
![]()
解得
![]()
根据KVL和KCL求得
![]()
![]()
例2.图示电路![]() 时处于稳态,
时处于稳态,![]() 时开关断开。求初始值
时开关断开。求初始值![]() 、
、![]() 及开关两端电压
及开关两端电压![]() 。
。
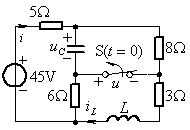
解:![]() 时电容处于开路,电感处于短路,
时电容处于开路,电感处于短路,![]() 电阻与
电阻与![]() 电阻相并联,所以
电阻相并联,所以
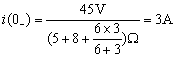
![]()
![]()
由换路定律得
![]() ,
,![]()
由KVL得开关电压
![]()
