为正弦电压源：
开关接通后电路的微分方程和初始值分别为
非齐次微分方程的通解
由两个分量组成——此方程的任一特解
和与此方程对应的齐次方程的通解
，即
(1) 求特解
凡是满足微分方程的解均可作为特解。显然，在
作用下的正弦稳态解也满足方程，可作为特解。求正弦稳态解宜用相量分析法，微分方程对应的相量方程
故电流
的振幅相量为
式中，
是图示RL串联电路的阻抗。特解时域表达式为
(2) 求对应的齐次微分方程的通解
齐次微分方程为
其通解为 
(3) 非齐次微分方程的通解
将
和
代入，得
(4) 确定积分常数
根据初始条件，
时
得 
时的电流波形
将
代入，得到非齐次微分方程的通解
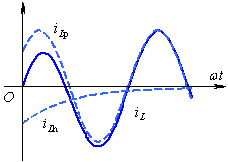
右图中画出了
时
、
和
的波形。
时的电流波形
例2.图(a)所示电路，开关原是接通的，
时断开，已知
。求电压
。
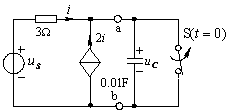
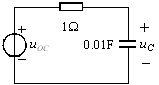
(a) (b)
解：
时电路为零状态，由换路定律得：
时为简化计算，先将ab左边电路化为戴维南电路形式。
当ab端开路时，由 
，得
所以开路电压 
当ab端短路时，
，
故等效电阻 
，
时等效电路如图(b)所示。电路时间常数为
。
用相量法计算强制分量
因此 
代入通解公式得：
V
例3.图示电路原处于稳态，
时开关打开。要求在
时满足
，求电路参数应满足的关系。
解：
， 
分析得知：电容一阶电路属于零状态响应；
电感一阶电路属于零输入响应；
根据KVL，列写方程如下：
(1)
(2)
由式(1)解得 
(3)
(4)
由式(2)又解得 
(5)
