1.动态电路
1）电路分类: 电路可按电源类型（DC,AC 等）；按元件类型；按电路所处状态分类。
电容元件和电感元件的电压与电流的关系都是导数或积分关系，称为动态元件。含有动态元件的电路称为动态电路，如(a)图。只含电阻和电源的电路就称为电阻电路，如(b)图。
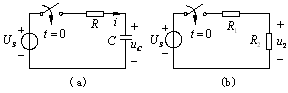
图1 动态电路和电阻电路
2）稳态和暂态
稳态：前面各章介绍的直流电路、正弦电流电路和非正弦周期电流电路中，电流和电压是常量或是周期量。电路的这种工作状态称为稳定状态，简称稳态。
换路：实际电路工作时总要发生变动如开关通断、电源值突变、元件参数变动，事故或干扰都会引起电流、电压的变化。引起电路工作状态变动的因素统称为换路。
暂态：动态电路换路之后，动态元件的储能也要发生变化。实际动态元件吸收或释放一定的能量是不可能瞬间完成的，需要经历一段过渡过程，电路此时的工作状态称为暂态，如图 (a)。
而电阻电路换路后，电压
便立即跃变到新的稳态值，如图 (b)所示。
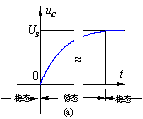
图2 稳态与暂态
2.时域分析法
本章将要分析动态电路在暂态过程中电压、电流的变化规律。电路方程都是以时间
为主变量的微分方程。例如图10.1 (a)所示电路换路后的KVL方程为
(1)
式中，代
得到
(2)
是常系数线性一阶微分方程。微分方程定解需要初始条件，即方程中待求变量在换路后瞬间的初始值。设电路在
时发生换路，用
和
分别表示换路前和换路后瞬间，则可用
、
、
、
表示电路变量的初始值。换路之后，电路量将从其初始值开始变动。以时间
为主变量列写电路的微分方程并确定初始条件，通过求解微分方程获得电压、电流的时间函数的分析方法称为时域分析法。