|
1.异步电机在两相任意旋转坐标系(dq坐标系)上的数学模型 |
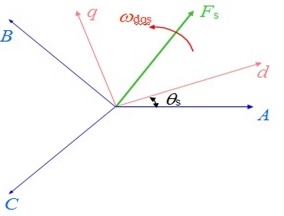 |
|
变换过程 |
| 具体的变换运算比较复杂, |
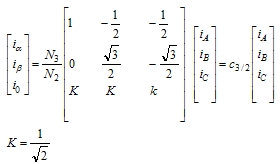 |
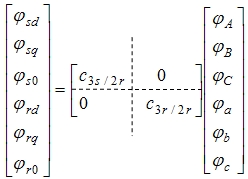
| 根据式(6-98)另0轴为假想轴d轴和A轴夹角为 θ 可得: |
| 写成矩阵形式: |
 |
| 合并以上两个方程式得三相静止ABC坐标系到两项旋转dq0坐标系的变换式 |
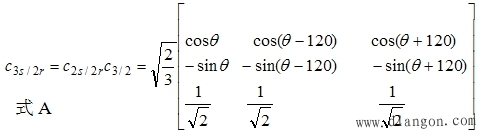 |
|
(1)磁链方程 |
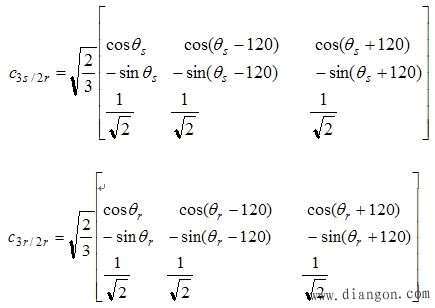 |
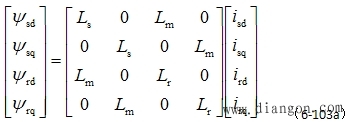
| 则磁链的变换式为: |
 |
|
把定子和转子的磁链表达成电感阵和电流向量乘积,在用 |
 |
|
磁链的零轴分量为 |
| 控制有关。 代入参数计算,并去掉零轴分量则dq坐标系磁链方程为 |
 |
| 或写成 |
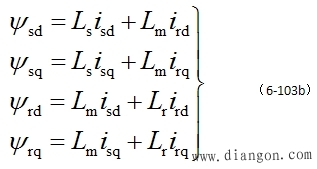 |
| 式中 |
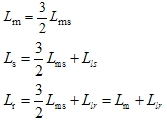 |
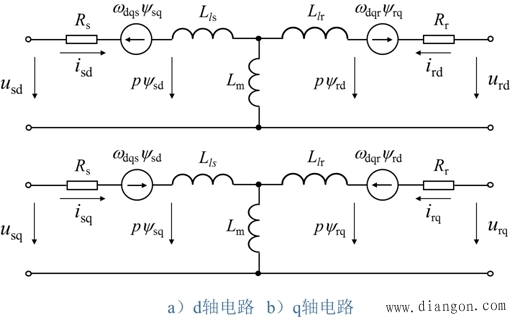
| —— dq坐标系定子与转子同轴等效绕组间的互感; —— dq坐标系定子等效两相绕组的自感; ——dq坐标系转子等效两相绕组的自感。 异步电机在两相旋转坐标系dq上的物理模型 |
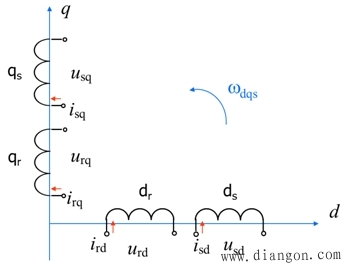 |
| 图6-50 异步电动机在两相旋转坐标系dq上的物理模型 |
| (2)电压方程 利用上式A得定子电压变换的关系为 |
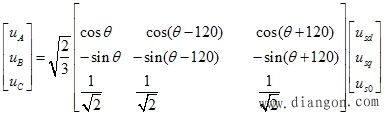 |
| 先讨论A相的关系 |
| 同理 |
| 在ABC坐标系下A相的电压方程, |
| 代入 |
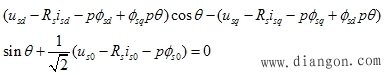 |
由于 |
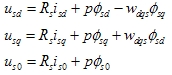 |
| 同理转子电压方程为 |
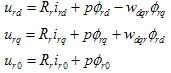 |
| 式中 |
| 同理利用B相和C相的电压方程求出的结果与上面一致。 (2)电压方程 上面的方程整理有定子和转子的电压方程 |
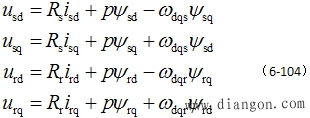 |
 |
| 令 |
 |
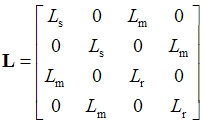 |
| 旋转电动势向量 |
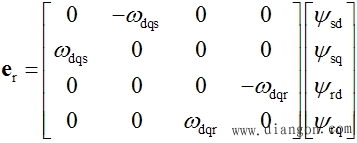 |
| 则式(6-106a)变成 |
|
这就是异步电机非线性动态电压方程式。与第6.6.2节中ABC坐标系方程不同的是:此处电感矩阵 L 变成 4 |
| dq坐标系上的转矩方程为 运动方程与坐标变换无关,仍为 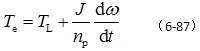 其中 阶数下降,但非线性、强耦合、多变量性质未变。 异步电机在dq坐标系上的动态等效电路 |
 |
| 2. 异步电机在 在静止坐标系 |
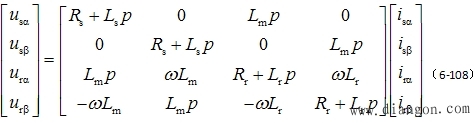 |
| 而式(6-103a)的磁链方程改为 |
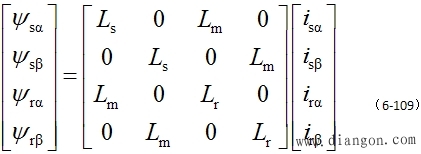 |
| 利用两相旋转变换阵 |
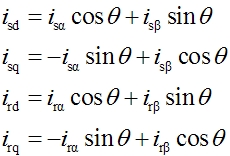 |
| 代入式(6-107)并整理后,即得到 |
|
式(6-108)~式(6-110)再加上运动方程式便成为 |
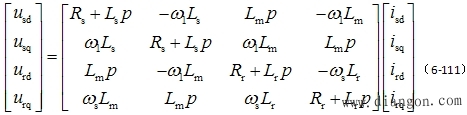 |
|
磁链方程、转矩方程和运动方程均不变。 |
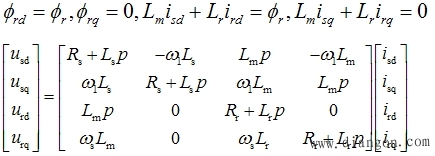 |
| 三四行出现零元素,减少了耦合,简化了模型 上式中解得 |
|
这个关系和直流电机的转矩方程非常接近了,如果是鼠笼电机结果会更加简单。 |
导读:目前正在解读《三相异步电动机在两相坐标系上的数学模型》的相关信息,《三相异步电动机在两相坐标系上的数学模型》是由用户自行发布的知识型内容!下面请观看由(电工学习网 - www.9pbb.com)用户发布《三相异步电动机在两相坐标系上的数学模型》的详细说明。
提醒:《三相异步电动机在两相坐标系上的数学模型》最后刷新时间 2023-07-10 04:01:19,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《三相异步电动机在两相坐标系上的数学模型》该内容的真实性请自行鉴别。
