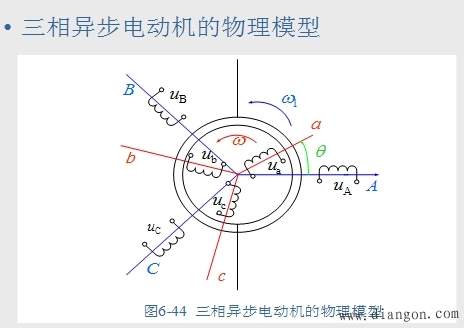
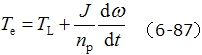|
假设条件: |
 |
| 1. 电压方程 三相定子绕组的电压平衡方程为 : |
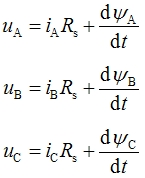 |
| 电压方程(续) 与此相应,三相转子绕组折算到定子侧后的电压方程为: |
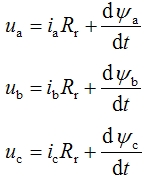 |
| 电压方程的矩阵形式 将电压方程写成矩阵形式,并以微分算子 p 代替微分符号 d /dt |
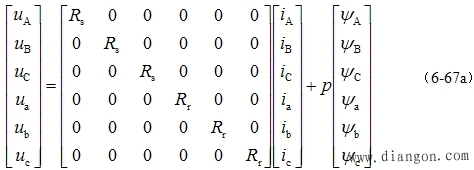 |
| 或写成 |
| 2. 磁链方程 每个绕组的磁链是它本身的自感磁链和其它绕组对它的互感磁链之和,因此,六个绕组的磁链可表达为 : |
 |
| 或写成 |
|
电感矩阵 |
| 自感表达式 对于每一相绕组来说,它所交链的磁通是互感磁通与漏感磁通之和,因此,定子各相自感为: |
| 转子各相自感为 : |
|
互感表达式 |
| 于是, |
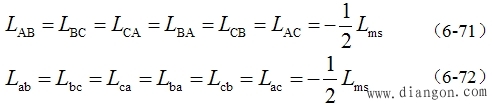 |
| 第二类变化位置绕组的互感 定、转子绕组间的互感,由于相互间位置的变化(见图6-44),可分别表示为: |
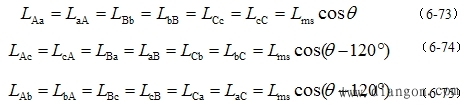 |
|
当定、转子两相绕组轴线一致时,两者之间的互感值最大,就是每相最大互感 Lms 。 |
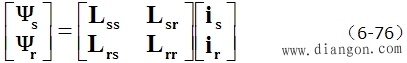 |
| 式中 |
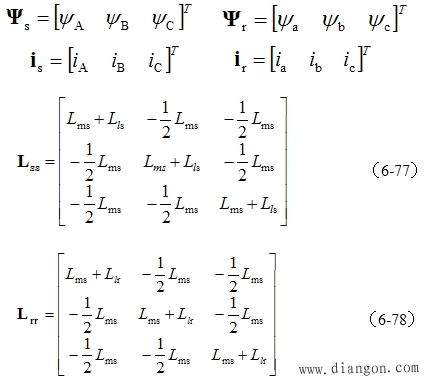 |
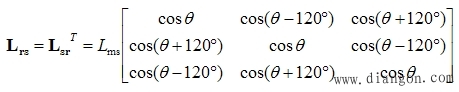 |
|
值得注意的是, |
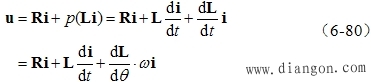 |
|
式中, |
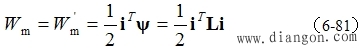 |
| 而电磁转矩等于机械角位移变化时磁共能的变化率(电流约束为常值),且机械角位移 |
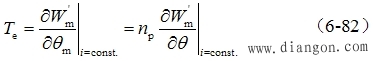 |
| 转矩方程的矩阵形式 将式(6-81)代入式(6-82),并考虑到电感的分块矩阵关系式(6-77)~(6-79),得: |
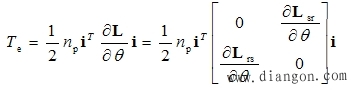 |
| 又由于 |
| 代入式(6-83)得: |
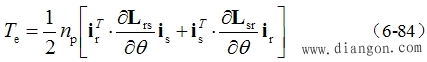 |
| 该方程适用变压变频器供电含有电流谐波三相异步电动机 转矩方程的三相坐标系形式 以式(6-79)代入式(6-84)并展开后,舍去负号,意即电磁转矩的正方向为使 q 减小的方向,则 |
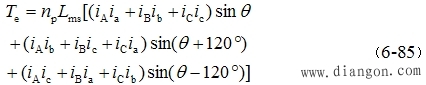 |
|
4. 电力拖动系统运动方程 |
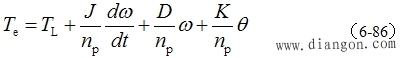 |
|
TL —— 负载阻转矩; |
|
5. 三相异步电机的数学模型 |
| 异步电机的多变量非线性动态结构图 |
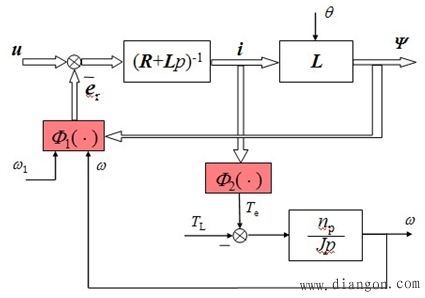 |
导读:目前正在解读《三相异步电动机的多变量非线性数学模型》的相关信息,《三相异步电动机的多变量非线性数学模型》是由用户自行发布的知识型内容!下面请观看由(电工学习网 - www.9pbb.com)用户发布《三相异步电动机的多变量非线性数学模型》的详细说明。
提醒:《三相异步电动机的多变量非线性数学模型》最后刷新时间 2023-07-10 04:01:19,本站为公益型个人网站,仅供个人学习和记录信息,不进行任何商业性质的盈利。如果内容、图片资源失效或内容涉及侵权,请反馈至,我们会及时处理。本站只保证内容的可读性,无法保证真实性,《三相异步电动机的多变量非线性数学模型》该内容的真实性请自行鉴别。