回路电流法

网孔电流法只适用于平面图，回路电流法既适用平面图，也适用非平面图。

1、回路电流法的原理

一个联通图，支路数 b ，节点数 n ，树支数 ( n - 1 ) ，连支数 b - ( n - 1 )；

选定一个树，加上一个连支，就构成一个回路，指定回路电流为 i _l1，也称为连支电流。对此回路应用 KVL ，得一 KVL 方程；

加上第二个连支，就构成第二个回路，指定回路电流为 i _l2，对此回路应用 KVL ，又得一 KVL 方程；

…………

最后得到：(b － n + 1) 个回路电流变量，和同样多的 KVL 方程；

连立求解得各回路/连支电流；

再叠加求出各支路电流。

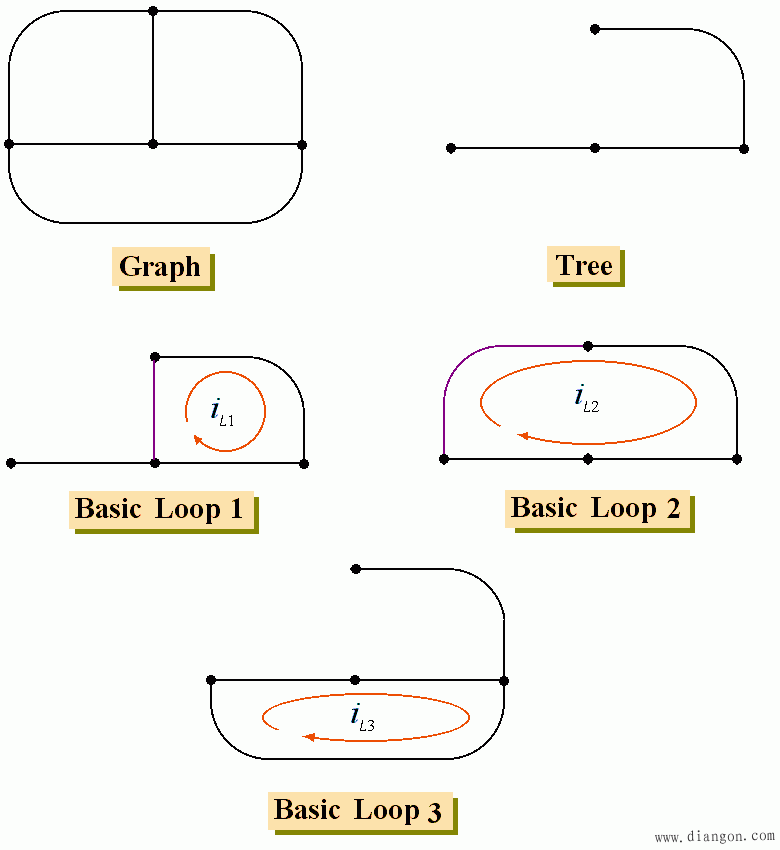
如果象下图粗线所示选取树，则基本回路就是三个网孔。这说明回路电流法比网孔电流法更普遍。

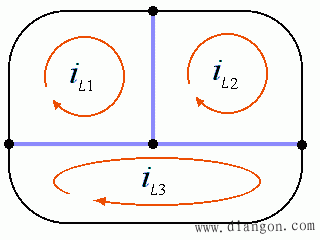
2、举例

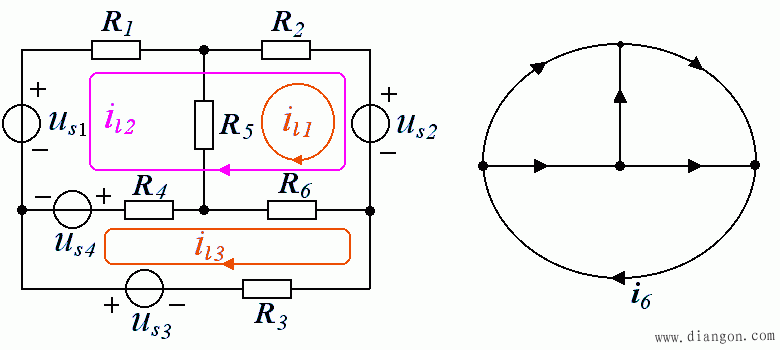
类似，R ₁₁称为自阻，R ₁₂称为互阻。自阻恒取 “＋” ，互阻符号取法：当回路电流方向与支路电流方向一致时取 “＋” ，否则取 “－” 。电压源符号同网孔电流法。

3、无伴电流源的处理

问题的提出：回路电流法是基于KVL方程的，即：

Σ u _k ＝ 0

但方程中并没有未知量 u_k ，而是用回路电流 i_lk 表示每一个支路的电压 u _k 的。如果某条支路电压不能用回路电流表示出来，怎么办？例如只有一个电流源？

无伴电流源: 无并联电阻的电流源就称为无伴电流源。

处理方法:

除将回路电流 i_lk 作为未知量外，将无伴电流源两端的电压 u 也作为一个未知变量列入方程，同时再增加一个该支路的电流方程 i_k ＝ i_s。这样，虽然多了一个变量，但又多了一个方程，且无伴电流源所在支路的电流为已知。

4、举例

求如下图示电路中的电流 I₁。

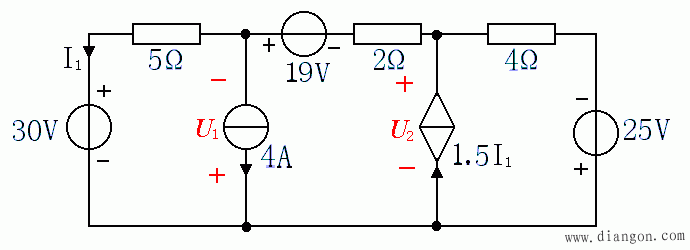
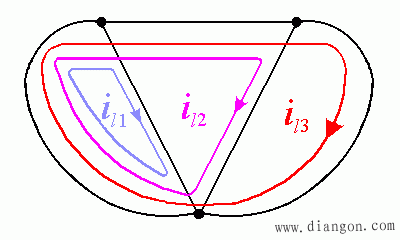
b = 5 ， n ＝ 3 ， b － n ＋ 1 ＝ 3 ；
未知量：5 个 ， 方程 5 个 ：

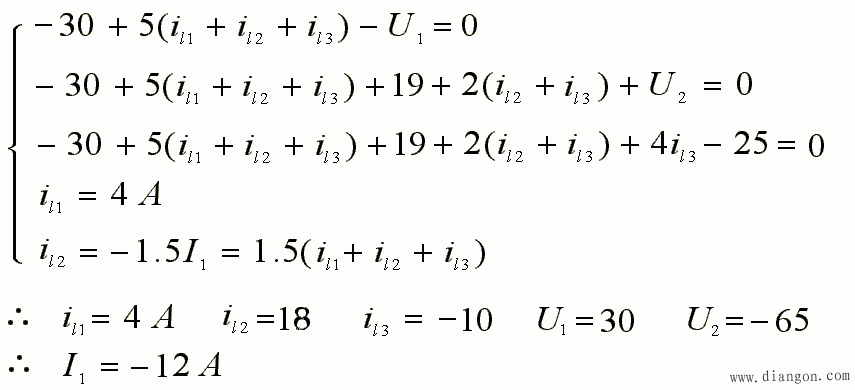
如果选取如下所示回路，问题变得更简单：4 个未知量，4 个方程：

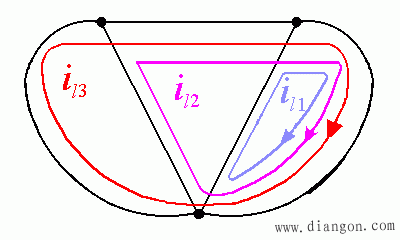
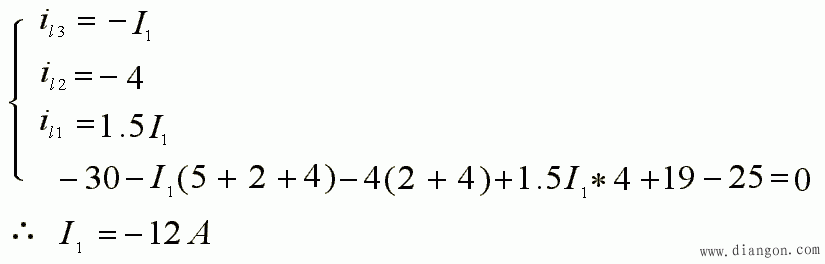
支路电流同上。