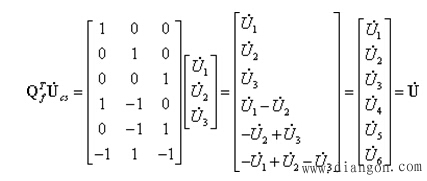割集电压法分析电路问题可以看作是节点法的一种推广。第一章已介绍过割集的定义、基本概念和初步应用。割集与支路之间的联系可以用一个矩阵
来描述。矩阵的行号对应着割集号，矩阵的列号对应于支路，矩阵中的元素
作如下定义：
这样建立的矩阵称为割集矩阵。通常对于一定的电路，可以选择许多不同的割集。但在用割集电压法解题时，只有一组独立的割集电压方程才有意义。因此，与选择独立回路相类似，实际应用中往往选择单树支割集作为一组独立的割集。当选用单树支割集时，这样建立的割集矩阵称为基本割集矩阵，记作
。为
阶矩阵。
对于图1所示的网络，若选择1、2、3支路为树，单树支割集及方向如图示，可写出其基本割集矩阵为：
上式右半部分为一单位矩阵。一般当支路编号严格按照先树支后连支编号且顺次列写，割集方向取树支方向时，中对应树支元素的子矩阵必是一个
阶单位矩阵，可表示为：
（2）
式中
表示由连支元素组成的割集子矩阵。
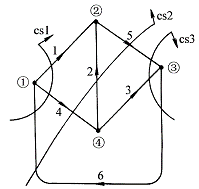
图 1
割集可以看成是一个广义的节点。由割集矩阵中元素的定义可知，割集矩阵的每一行元素反映了穿过该割集表面的所有支路及其方向。若用左乘支路电流列向量
，则其乘积的每一行之和恰为穿过该割集表面的支路电流的代数和。由基尔霍夫定律可知，任一广义节点（割集包围的部分）的电流代数和恒为零，因此与支路电流列向量
之积为零向量，即有：
（3） 或 
（4）
上式是广义节点的基尔霍夫电流定律的矩阵形式。
对于图1所示的网络，其支路电流列向量为
，前面已写出其基本割集矩阵。用左乘
，可得：
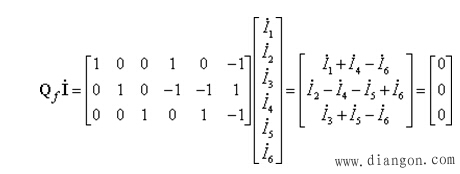
在用割集电压法分析网络问题时，割集电压作为一组独立变量。若选择单树支割集为基本割集，则割集电压即为树支电压，即有
。类似于节点电位与支路电压之间的关系，若用割集矩阵的转置矩阵
左乘割集电压列向量
，其乘积为支路电压列向量u，即有：
（5）
此式反映了割集电压与支路电压之间的关系。例如对于图7-4-1所示的网络，选单树支割集为基本割集，则割集电压列向量即为树支电压：
用左乘
，可得：
