对于同一个电路,若各支路,节点的编号及方向均相同时,其列写出的关联矩阵,回路矩阵和割集矩阵之间存在着一定的联系。
对于图1所示的有向图,选支路1、2、3为树支,作单树支割集如图所示,则可写出其基本回路矩阵与基本割集矩阵如下:
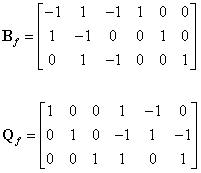
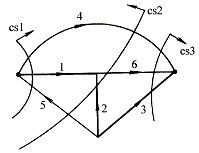
图 1
用![]() 左乘
左乘![]() ,可得:
,可得:
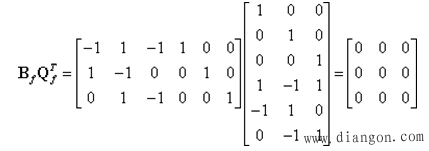
即有:
![]() (1)
(1)
由矩阵性质可得另一形式为:
![]() (72)
(72)
此二式反映了相同编号的网络中,基本割集矩阵![]() 与基本回路矩阵
与基本回路矩阵![]() 之间的关系。
之间的关系。
对于式1的一般证明可简略描述如下:令![]() ,则D中任一元素为
,则D中任一元素为![]() ,下标j表示第j条单连支回路,k表示第k个割集,而
,下标j表示第j条单连支回路,k表示第k个割集,而![]() 则表示把
则表示把![]() 第j回路中i支路元素与
第j回路中i支路元素与![]() 第k割集中i支路元素相乘。显然,若i支路不是同时包含在j回路与k割集中,则其乘积必为零。而同时包含在j回路与k割集中的支路条数必为偶数。因为若移去k割集的所有支路,则电路分为独立的两部分。若闭合回路跨越两部分电路,显然其连接两部分的支路条数(包含在k割集中)必为偶数条。例如对于图1所示的网络,同时包含在割集1与回路1(由支路4组成的单连支回路)中的支路为4与1。
第k割集中i支路元素相乘。显然,若i支路不是同时包含在j回路与k割集中,则其乘积必为零。而同时包含在j回路与k割集中的支路条数必为偶数。因为若移去k割集的所有支路,则电路分为独立的两部分。若闭合回路跨越两部分电路,显然其连接两部分的支路条数(包含在k割集中)必为偶数条。例如对于图1所示的网络,同时包含在割集1与回路1(由支路4组成的单连支回路)中的支路为4与1。
对于成对出现在回路和割集中的支路,如果二条支路方向与回路一致,(此时![]() 对应行中二个元素
对应行中二个元素![]() 同号),则该二条支路与割集方向必一正一反(此时
同号),则该二条支路与割集方向必一正一反(此时![]() 对应行中二个元素
对应行中二个元素![]() 异号),则
异号),则![]() 的值必为零。反之,若二条支路方向与回路方向一正一反,则相对于割集方向必同号,其乘积
的值必为零。反之,若二条支路方向与回路方向一正一反,则相对于割集方向必同号,其乘积![]() 亦为零。可见矩阵D中元素均为零,从而可推出式(1)。
亦为零。可见矩阵D中元素均为零,从而可推出式(1)。
若网络支路编号严格按先树支后连支编排,则式(1)可写为:
![]()
即有:
![]() (3)
(3)
式中,![]() 表示由树支组成的回路矩阵子矩阵;
表示由树支组成的回路矩阵子矩阵;![]() 表示由连支组成的割集矩阵子矩阵。
表示由连支组成的割集矩阵子矩阵。
对于图1的电路,若设节点4为参考节点,写出它的关联矩阵为:

用A左乘![]() ,得:
,得:
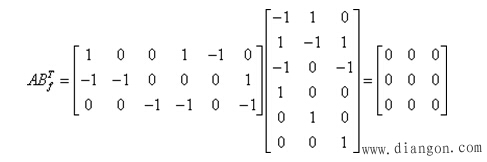
即有:
![]() (7-5-4) 或
(7-5-4) 或 ![]() (5)
(5)
实际上若选择割集只包围一个节点,且割集方向离开节点,则这样组成的割集即为关联矩阵A,即是说关联矩阵无非是割集矩阵的一种形式。由式(1)即可知式(4)成立。
如果支路编号按先树支后连支方式,则关联矩阵可表示为![]() ,其中
,其中![]() 表示由所有树支元素组成的子矩阵,
表示由所有树支元素组成的子矩阵,![]() 表示由连支元素组成的子矩阵。式(4)可描述为:
表示由连支元素组成的子矩阵。式(4)可描述为:
![]()
上式左乘![]() ,可得:
,可得:
![]()
即有:
![]() (6)
(6)
据此,基本回路矩阵可写成:
![]() (7)
(7)
从该表达式可见,对于一个支路编号采用先树支后连支方式的电路,其基本回路矩阵![]() 可通过关联矩阵求得。
可通过关联矩阵求得。
同理,由式(3)及式(6)可得,![]() ,因此基本割集矩阵又可表达为:
,因此基本割集矩阵又可表达为:![]() (8)
(8)
由式可知,基本割集矩阵可由关联矩阵求得。
当采用计算机辅助计算建立状态方程时,直接写回路矩阵或割集矩阵往往比较困难,而推求关联矩阵却很方便。因此在实际应用时往往由关联矩阵通过式(7)和式(8)求得回路矩阵与割集矩阵。
