对于非正弦周期信号激励的稳态电路，无法用直流电路或正弦交流电路的计算方法来分析计算，而必须先把非正弦周期信号激励用傅里叶级数分解为不同频率的正弦分量之和，然后再分别计算各个频率分量激励下的电路响应。最后用叠加定理把各响应分量进行叠加获得稳态响应。其计算过程的主要步骤可分为三步：
（1）把给定的非正弦周期激励源分解为傅里叶级数表达式，即分解为直流分量与各次谐波分量之和，根据展开式各项收敛性及所需精度确定所需谐波项数；
（2）分别计算直流分量和各频率谐波分量激励下的电路响应。直流分量用直流电路分析方法，此时电感短路、电容开路；对于不同频率的正弦分量，采用正弦电路相量分析计算方法，这时需注意电路的阻抗随频率而变化，各分量单独计算时应作出对应电路图；
（3）应用叠加定理把输出响应的各谐波分量相加得到总的响应值，注意叠加前应把各谐波响应表达成时域瞬时式（因为不同频率的相量式相加是无意义的）。
下面用具体例子来说明线性电路的周期非正弦稳态分析。
例1 电路如图1所示，已知
，
，
，电源电压
，基波角频率
，试求流过电阻的电流
及电感两端电压
。
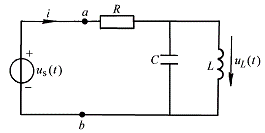
图 1
解：本题的激励电压源已分解成各次谐波分量，因此可直接进行各次谐波的计算。对于直流分量的计算，可用一般直流电路的解题方法，画出对应直流电路如图2a所示，已知
，则得
对于基波分量
，其对应电路如2b所示，
，ab端入端阻抗：
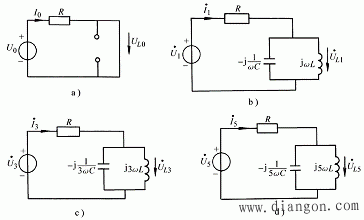
图 2
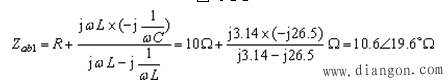
电感两端电压：
即有：
，
对于三次谐波分量，其等效电路如图6-2-2c所示，
，其入端阻抗为：
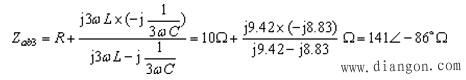
电感两端电压：
即有：
，
对于五次谐波，等效电路如图6-2-2d所示，有
，ab端入端阻抗为：
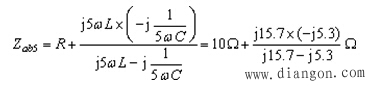
电感两端电压：
即有：
，
最后得到流经电阻的电流值为：
从计算结果可看出，电路对不同频率的分量呈现不同的特性。当三次谐波激励时，入端阻抗特别大，因此产生的电流分量较小，这是由于接近电路谐振频率点的缘故。
下面讨论非正弦周期信号的有效值和功率问题。前面已定义了周期信号的有效值为：
对于非正弦周期信号电流，可展为傅里叶级数：
代入有效值表达式有：
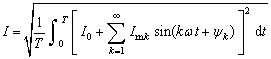
把根号内的平方展开，可得两类表达式，一类是同频率电流分量的平方，可计算得：
第二类为不同频率的电流乘积，由三角函数的正交性可知，不同频率的二个正弦函数乘积在
上积分为零，即有：
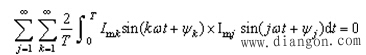
于是可得周期非正弦交流电流的有效值为：
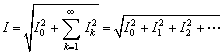（6-2-1）
式中，Ik为各次谐波的有效值。同理可推得非正弦周期电压有效值为：
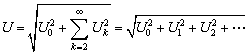（6-2-2）
非正弦周期信号的功率：
，
式中，
，
平均功率为：
将
、展开式代入，其乘积的表达式由同频率正弦量与不同频率正弦量乘积组成，考虑到三角函数在上的正交性，可推得：
（3）
式中，
为k次谐波电压与电流相位差。由式可知，非正弦信号的平均功率等于各谐波信号平均功率之和。