基尔霍夫电压定律(简称KVL定律)是用来确定回路中各段电压间关系的。如果从回路中任意一点出发,以顺时针方向或逆时针方向沿回路循行一周,则在这个方向上的电位降之和应该等于电位升之和,回到原来的出发点时,该点的电位是不会发生变化的。此即电路中任意一点的瞬时电位具有单值性的结果。
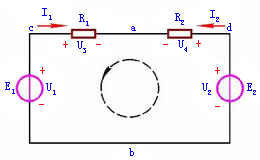
今以图1所示的回路为例,图中电源电动势、电流和各段电压的参考方向均已标出。按照虚线所示方向循行一周,根据电压的参考方向可列出
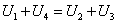
或将上式改写为
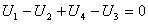
即
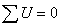 (1)
(1)
就是在任一瞬时,沿任一回路循行方向(顺时针方向或逆时针方向),回路中各段电压的代数和恒等于零。如果规定电位降取正号,则电位升就取负号。
 |
|
图1 回路 |
以后在电阻电路中列KVL方程时,直接将欧姆定律代入,上式也可改写为
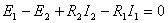
即
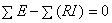 (2)
(2)
此为基尔霍夫电压定律在电阻电路中的另一种表达式,就是在任一回路循行方向上,回路中电动势的代数和等于电阻上电压降的代数和。在这里,凡是电动势的参考方向与所选回路循行方向相反者,则取正号,一致者则取负号,凡是电流的参考方向与回路循行方向一致者,则该电流在电阻上所产生的电压降取正号,相反者则取负号。
基尔霍夫电压定律不仅应用于闭合回路,也可以把它推广应用于回路的部分电路。现以图1.14所示的两个电路为例,根据基尔霍夫电压定律列出式子。
 |
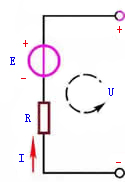 |
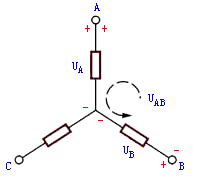
| (a) | (b) |
|
图2基尔霍夫电压定律的推广应用 | |
对图2(a)所示电路(各支路的元件是任意的)可列出
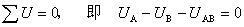
或
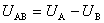
对图2(b)的电路可列出
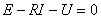
或
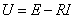
这也就是一段有源(有电源)电路的欧姆定律的表达式。
应该指出,图1所举的是直流电阻电路,但是基尔霍夫两个定律具有普遍性,它们适用于有各种不同元件所构成的电路,也适用于任一瞬时任何变化的电流和电压。
列方程时,不论是应用基尔霍夫定律或欧姆定律,首先都要在电路图上标出电流、电压或电动势的参考方向;因为所列方程中各项前的正负号是由它们的参考方向决定的,如果参考方向选得相反,则会相差一个负号。
