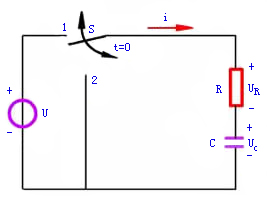
图1所示是一RC串联电路。可分三种响应对其进行暂态分析。
1、零状态响应
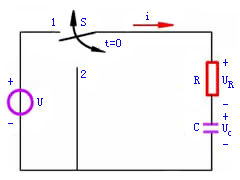 |
|
图1 RC电路 |
所谓RC电路的零状态,是指换路前电容元件未储有能量,即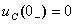 。在此条件下,由电源激励所产生的电路的响应,称为零状态响应。
。在此条件下,由电源激励所产生的电路的响应,称为零状态响应。
在图1中,如果在t=0时将开关S合到位置1上,电路即与一恒定电压为U的电压源接通,对电容元件开始充电,其上电压为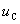 。
。
根据基尔霍夫电压定律,列出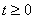 时电路的微分方程
时电路的微分方程
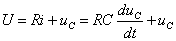 (1)
(1)
上式的通解有两个部分:一个是特解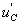 ,一个是补函数
,一个是补函数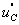 。
。
特解取电路的稳态值,或称稳态分量,即
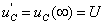
补函数是齐次微分方程
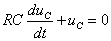
的通解,其形式为
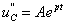
代入上式,得特征方程
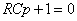
其根为
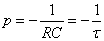
式中,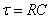 ,它具有时间的量纲,所以称为RC电路的时间常数。
,它具有时间的量纲,所以称为RC电路的时间常数。
因此,式(1.37)的通解为
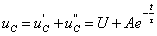
 |
| 图2零状态响应 |
设换路前电容元件未储有能量,即初始值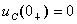 ,则
,则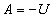 ,于是得
,于是得
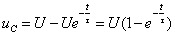 (2)
(2)
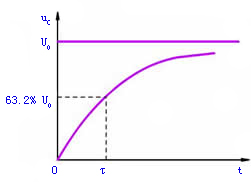
其随时间的变化曲线如图2所示。
当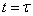 时
时
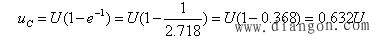
即从t=0经过一个τ的时间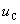 增长到稳定值U的63.2%。
增长到稳定值U的63.2%。
从理论上讲,电路只有经过t=∞的时间才能达到稳定。但是,由于指数曲线开始变化较快,而后逐渐缓慢。所以,实际上经t=5τ的时间,就足可认为达到稳定状态了。τ愈小,曲线的增长就愈快。
由式(2)也可求出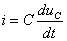 和
和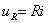 ,即
,即
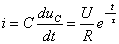 (3)
(3)
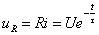 (4)
(4)
2、零输入响应
所谓RC电路的零输入,是指无电源激励,输入信号为零。在此条件下,由电容元件的初始状态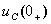 所产生的电路的响应,称为零输入响应。
所产生的电路的响应,称为零输入响应。
如果在图3中,当电容元件充电到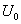 时,即将开关S从位置1合到2,脱离电源(输入为零),电容元件开始放电,稳态值
时,即将开关S从位置1合到2,脱离电源(输入为零),电容元件开始放电,稳态值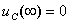 [初始值
[初始值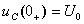 ],则经求解可得
],则经求解可得
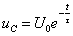 (5)
(5)
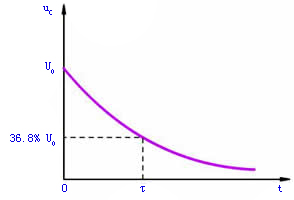
其随时间的变化曲线如图4所示。
 |
 |
|
图3 RC电路 |
图4 零输入响应 |
当t=τ时
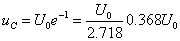
即从t=0经过一个τ的时间uC衰减到初始值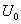 的36.8%。τ愈小,衰减愈快。
的36.8%。τ愈小,衰减愈快。
由式 (5)也可求出

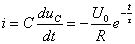 (6)
(6)
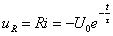 (7)
(7)
上两式中的负号表示放电电流的实际方向与图1中所选定的参考方向相反。
3、全响应
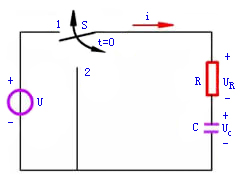
如果在图5中,电容元件初始电压为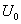 ,t=0时,将开关S从位置合到2,电路即进入全响应。
,t=0时,将开关S从位置合到2,电路即进入全响应。
 |
|
图5RC电路 |
所谓RC电路的全响应,是指电源激励和电容元件的初始状态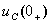 均不为零时电路
均不为零时电路
的响应,也就是零状态响应与零输入响应两者的叠加。
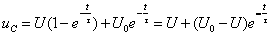 (8)
(8)
由式 (8)可写出分析一阶线性电路暂态过程中任意变量的一般公式,即
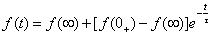 (9)
(9)
只要求得初始值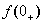 、稳态值
、稳态值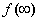 和电路时间常数τ这三个“要素”,就能直接写出电路的响应(电压或电流)。这就是一阶线性电路暂态分析的三要素法。
和电路时间常数τ这三个“要素”,就能直接写出电路的响应(电压或电流)。这就是一阶线性电路暂态分析的三要素法。
