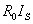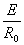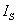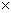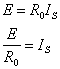一个电源可以用两种不同的电路模型来表示。一种是用电压的形式来表示,称为电压源;一种是用电流的形式来表示,称为电流源。
1、电压源
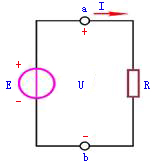
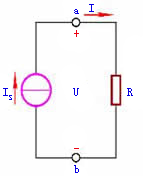
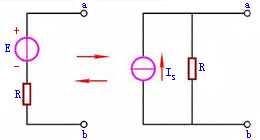
任何一个电源,例如发电机、电池或各种信号源,都含有电动势E和内阻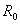 。在分析与计算电路时,往往把它们分开,组成的电路模型如图1.17所示,此即电压源。图中,U是电源端电压,R是负载电阻,I是负载电流。
。在分析与计算电路时,往往把它们分开,组成的电路模型如图1.17所示,此即电压源。图中,U是电源端电压,R是负载电阻,I是负载电流。
根据图1所示的电路,可得出
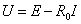 (1)
(1)
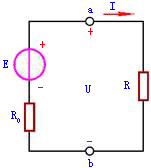
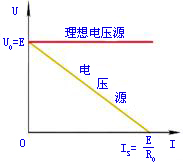
由此可作出电压源的外特性曲线,如图2所示。当电压源开路时,I=0,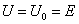 ;当短路时,U=0,
;当短路时,U=0,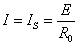 。内阻
。内阻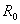 愈小,则直线愈平。
愈小,则直线愈平。
 |
 |
 |
| 图1电压源电路图 | 2电压源和理想图 | 3理想电压源电路 |
|
电压源的外特性曲线 | ||
当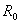 =0时,电压U恒等于电动势E,是一定值,而其中的电流I则是任意的,由负载电阻R及电压U本身确定。这样的电源称为理想电压源或恒压源,其符号及电路如图3所示。它的外特性曲线将是与横轴平行的一条直线,如图2所示。
=0时,电压U恒等于电动势E,是一定值,而其中的电流I则是任意的,由负载电阻R及电压U本身确定。这样的电源称为理想电压源或恒压源,其符号及电路如图3所示。它的外特性曲线将是与横轴平行的一条直线,如图2所示。
理想电压源是理想的电源。如果一个电源的内阻远小于负载电阻,即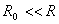 时,则内阻电压降
时,则内阻电压降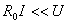 ,于是
,于是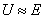 ,基本上恒定,可以认为是理想电压源。通常用的稳压电源也可认为是一个理想电压源。
,基本上恒定,可以认为是理想电压源。通常用的稳压电源也可认为是一个理想电压源。
2、电流源
电源除用电动势E和内阻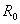 的电路模型来表示外,还可以用另一种电路模型来表示。
的电路模型来表示外,还可以用另一种电路模型来表示。
如将式(1)两端除以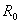 ,则得
,则得
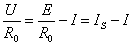
即
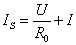 (2)
(2)
式中,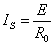 为电源的短路电流;I还是负载电流;而
为电源的短路电流;I还是负载电流;而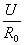 是引出的另一个电流。如用电路图表示,则如图4所示。
是引出的另一个电流。如用电路图表示,则如图4所示。
图4是用电流来表示的电源的电路模型,此即电流源,两条支路并联,其中电流分别为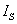 和
和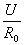 。对负载电阻R讲,和图1是一样的,其上电压U和通过的电流I未有改变。
。对负载电阻R讲,和图1是一样的,其上电压U和通过的电流I未有改变。
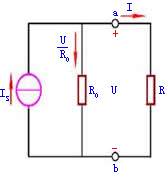
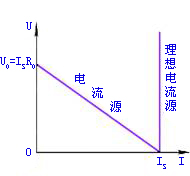
由式 (2)可作出电流源的外特性曲线,如图1.21所示。当电流源开路时,I=0,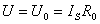 ;当短路时,U=0,I=
;当短路时,U=0,I=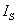 。内阻
。内阻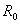 愈大,则直线愈陡。
愈大,则直线愈陡。
 |
 |
 |
| 图4 电流源电路 | 图5 电流源和理想 | 图6理想电流源电路 |
|
电流源的外特性曲线 | ||
当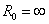 (相当于并联支路
(相当于并联支路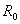 断开)时,电流I恒等于
断开)时,电流I恒等于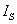 ,是一定值,而其两端的电压U则是任意的,由负载电阻R及电流
,是一定值,而其两端的电压U则是任意的,由负载电阻R及电流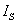 本身确定。这样的电源称为理想电流源或恒流源,其符号及电路如图6所示。它的外特性曲线将是与纵轴平行的一条直线,如图5所示。
本身确定。这样的电源称为理想电流源或恒流源,其符号及电路如图6所示。它的外特性曲线将是与纵轴平行的一条直线,如图5所示。
理想电流源也是理想的电源。如果一个电源的内阻远大于负载电阻,即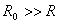 时,则
时,则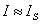 ,基本上恒定,可以认为是理想电流源。
,基本上恒定,可以认为是理想电流源。
3、电压源与电流源的等效变换
电压源的外特性(图2)和电流源的外特性(图5)是相同的。因此,电源的两种电路模型(图1和图4),即电压源和电流源,相互间是等效的,可以等效变换。
但是,电压源和电流源的等效关系只是对外电路而言的,至于对电源内部,则是不等效的。例如在图1中,当电压源开路时,I=0,电源内阻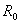 上不损耗功率;但在图4中,当电流源开路时,电源内部仍有电流,内阻
上不损耗功率;但在图4中,当电流源开路时,电源内部仍有电流,内阻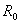 上有功率损耗。当电压源和电流源短路时也是这样,两者对外电路是等效的
上有功率损耗。当电压源和电流源短路时也是这样,两者对外电路是等效的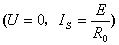 ,但电源内部的功率损耗也不一样,电压源有损耗,而电流源无损耗(
,但电源内部的功率损耗也不一样,电压源有损耗,而电流源无损耗( 被短路,其中不通过电流)。
被短路,其中不通过电流)。
 |
|
图7 电压源和电流源的等效变换 |
上面所讲的电源的两种电路模型,实际上,一种是电动势为E的理想电压源和内阻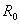 串联的电路(图1);一种是电流为
串联的电路(图1);一种是电流为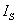 的理想电流源和
的理想电流源和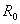 并联的电路(图4)。
并联的电路(图4)。
一般不限于内阻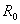 ,只要一个电动势为E的理想电压源和某个电阻R串联的电路,都可以化为一个电流为
,只要一个电动势为E的理想电压源和某个电阻R串联的电路,都可以化为一个电流为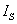 的理想电流源和这个电阻R并联的电路(图7),两者是等效的,其中
的理想电流源和这个电阻R并联的电路(图7),两者是等效的,其中
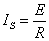 或
或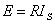 (3)
(3)
在分析与计算电路时,也可以用这种等效变换的方法。
但是,理想电压源和理想电流源本身之间没有等效的关系。因为对理想电压源(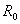 =0)讲,其短路电流
=0)讲,其短路电流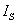 为无穷大,对理想电流源(
为无穷大,对理想电流源(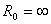 )讲,其开路电压
)讲,其开路电压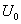 为无穷大,都不能得到有限的数值,故两者之间不存在等效变换的条件。
为无穷大,都不能得到有限的数值,故两者之间不存在等效变换的条件。
今列出表1将电压源和电流源作一对照。
|
表1电压源和电流源的对照 | |||||
| 电源状态 | 电压源 | 电流源 | 理想电压源 | 理想电流源 | |
|
开路 |
U |
E |
|
E |
|
|
I |
0 |
0 |
0 |
| |
|
短路 |
U |
0 |
0 |
|
0 |
|
I |
|
|
|
| |
|
等效条件 |
|
不等效 | |||