“图”的概念:对于任何一个由集总参数元件组成的电路,可以不问元件的性质,只考虑元件之间的联接关系,而将电路中的每个元件用一条线段代替,仍称之为支路,此线段可以是直线也可以是曲线;将每个元件的端点或若干个元件相连接的点(即节点)用一个圆点表示,仍称之为节点。将电路元件抽去,把每一条支路画成抽象的线段,仅有节点和支路的集合组成的电路图称之为电路的“图”,用“ G ” 表示。
例如图1 (a)是一个具有 6 个电阻元件, 2 个独立电源的电路。我们把元件的串联组合作为一条支路处理。 以此为根据画出电路的“图”如图 (b) 所示,我们还可以把 is2和 R2的并联组合化成串联组合,这样(b)图将成为(c)图。
在电路中还常要指定每一条支路的电流参考方向,电压取关联参考方向。标明各支路参考方向的“图”就称为“有向图”,未标明各支路参考方向的“图”就称为“无向图”。图( b )和图( c )为无向图,( d )为有向图。
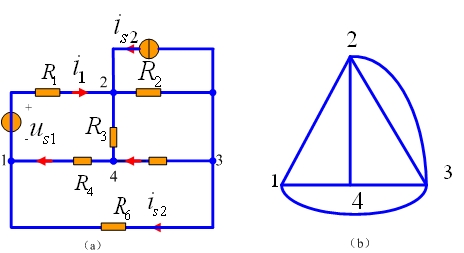
(a) (b)
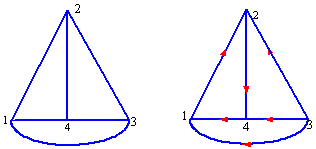
(c) (d)
图1 电路的“图”
第二 KCL 、 KVL 的独立方程数
1. KCL 的独立方程数
图 2 是某电路的有向图。该电路有 4 个节点, 6 条支路,编号如图所示。对节点 1 , 2 , 3 , 4 分别列出 KCL 方程:
节点 1 : ![]() ①
①
节点 2 : ![]() ②
②
节点 3 : ![]() ③
③
节点 4 : ![]() ④
④
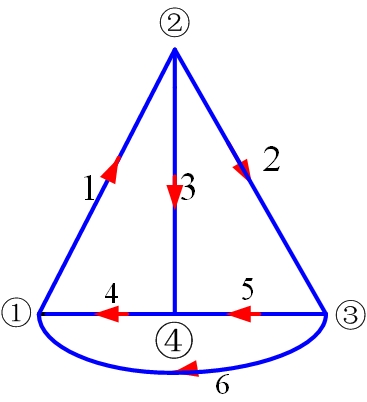
图2 KCL 的独立方程数
我们注意到对上述 4 个方程:①+②+③=④;①+②+④=③,依此类推,每一个方程都能由其余 3 个方程得到,也就是说在这 4 个方程中只有 3 个方程是彼此独立的。这是因为只有这 3 个方程包含其余两个方程没有涉及到的支路电流,所以这 3 个方程中的任何一个都不可能由另外两个方程导出,而第 4 个方程不可能有其余 3 个方程没有涉及到的新的支路出现。由此可见,具有 4 个节点的电路只能得到 3 个独立的 KCL 方程。可以证明,对于有 n 个节点的电路,独立节点方程数恒等于节点数减 1 ,即( n-1 )个,相应的( n-1 )个节点就称为独立节点。
2. KVL 的独立方程数
图 2 具有 7 个回路,我们选择如图 2-4-3 所示的 4 个回路,均按顺时针方向列出 KVL 方程:
左: ![]() ①
①
右: ![]() ②
②
下: ![]() ③
③
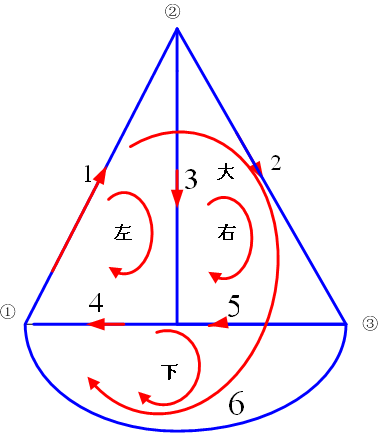
图3 KVL 的独立方程数
大: ![]() ④
④
上述方程① + ② + ③=④;① + ② - ④=③,以此类推,每一个方程都能由其它 3 个方程得到,也就是说在这 4 个方程中只有 3 个方程是相互独立的,这
是因为在这 4 个方程中每一条支路均用了两次,只有 3 个方程包含其余两个方程没有涉及到的新的支路压降。只有出现一个新的支路的回路才称为独立回路。对于上述具有 6 条支路、 4 个节点的复杂电路即使有 7 个回路,然而独立的回路数也只有 3 个,恰好等于节点数 4-1 。只有独立回路列出的 KVL 方程才是独立的。
可以证明:对于一般具有 b 条支路 n 个节点的电路,应用基尔霍夫电压定律所能得到的独立回路方程数为 [b-(n-1)] 。恰好等于一个平面电路的网孔数。而平面电路中每一个网孔必然是一个独立回路,也就是说应用基尔霍夫第二定律列出的独立回路方程数恒等于支路数减独立节点数即等于网孔数。 综上可见基尔霍夫电流定律和电压定律所列出的独立方程数恰好等于支路数,即
( n-1 ) +[b-(n-1)]=b 。
