由线性原件和独立电源（在这里受控源当电阻处理）组成的电路称为线性电路。独立电源是电路的输入，对电路起着激励（ excitation ）的作用。而电路中其它原件（或者其它部分）的电压和电流是激励引起的响应（ response ）。在线性电路中，响应和激励之间存在着线性关系。
例如，在图1 所示单一激励的线性电路中：
( 1 )
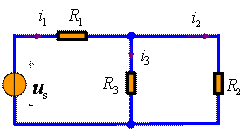
图1 比例性示例
由于R1、R2、R3均为常数，所以 
正比于 
，显然若 
增大 K 倍，
也增加 K 倍。在该电路的其它任何一处的电压和电流对激励都存在这种线性关
系，我们称之为线性电路的比例性或齐次性，即：
在线性电路中，当所有激励同时增大或缩小 K 倍时，响应也相应的增大或缩小 K 倍。
可表示为：
( 2 )
有两种关系需要注意：
(1) 激励是指独立源，且是所有激励同时增大或者缩小 K 倍。
(2) 当只有一个激励时，响应与激励成正比。
该性质给我们提供了解决节数很多的梯形网络问题的较简单方法，即倒退法。下面我们用实例说明这种方法的应用：
【例1 】 对于 例 图1 所示的电路 (1) 当端口电压 
=50V 时，求输出电压 
； (2) 计算端口等效电阻 
。
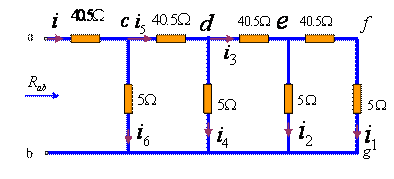
例图 1
解：
（ 1 ）此电路有 4 个节点（简单节点不计）， 4 个网孔。可以用前两章学过的各种方法求解，但是却很复杂，我们可以用线性电路的齐次性来解。先假定
= 1A ，则
=4.5V ， 
=45V ， 
， 
， 
， 
， 
而实际端口电压 
， 
所以由线性电路的齐次性可得：
， 
(2) 端口等效电阻： 
本题所指示的方法我们称之为倒退法。