含有动态元件(即储能元件)的电路称为动态电路(dynamic circuit)。由于动态元件的电压与电流之间呈导数关系或积分关系，根据基尔霍夫定律对动态电路列出的方程是微分方程或积分微分方程。以图1所示电路为例，根据基尔霍夫电压定律可得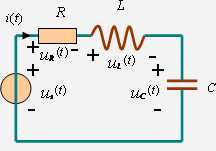
（1）
假设电路的待求变量是
，把电容元件的电压
电流关系 
图 1 简单动态电路
代入式 （1）经整理后得到
（2）
在电路分析中，作为输入激励的电压或电流可简称输入(input)，而作为待求响应(或变量)的电压或电流可简称输出(output)。
只含有一个激励源和一个输出变量的电路称为单输入—单输出电路(singal-input singal-outputcircuit)。式(2)是联系图1所示电路的输人
与输出
之间关系的单一变量微分方程，称为该电路的输人—输出方程。对于线性电路，输人—输出方程是常系数线性微分方程。
对于图1所示的电路，当求出
后，可应用元件的电压电流关系式 
求出电路中的电流和任一元件的电压。
可以证明有几个动态元件，其动态电路的输入输出方程就有几阶
对于任何一个已知的单输入—单输出的动态电路，应用基尔霍夫定律与电路 中各元件的电压电流关系，总可以求出其输人—输出方程。但是，电路越复杂，获得此方程所需要的工作量就越大。下面以图2所示电路为例说明复杂电路输入—输出方程的建立及输入—输出方程的一般形式。
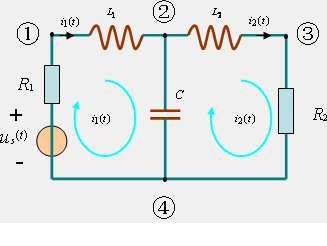
图 2 多回路的动态元件
图2是含有三个动态原件两个网孔四个节点的动态电路，应用§2—6的回路分析法可建立两个独立回路方程
（3a）
（3b）
由式(3)可知，对动态电路建立的回路方程是一组联立的积分微分方程。类似地，若对图2所示电路应用§2—7的节点分析法建立节点方程，则所得节点方程也是一组联立的积分微分方程。
现在假设电路的输出变量是回路电流
，从回路方程式(3)来推求图2所示单输入—单输出电路的输入—输出方程。
将式(3a)与式(3b)相加，得
（4）
将式 （3a）对t 求导，得
由此式可得 
（5）
将式 （5）对t 求导，得
（6）
将式（5）与式（6）代入式（4），经移项整理后，得到
（7）
式（7)就是图2所示电路以
作为输出变量的输入—输出方程。这是一个三阶的常系数线性微分方程，其中
和
的系数及其各阶导数的系数都是常数。以回路电流
作为输出变量，亦可得到类似的输入—输出方程。
由以上分析可以看出：对一般动态电路建立的电路方程是一组联立的微分方程，或一组联立的积分微分方程[见式(4—4—3)]。由此联立方程组出发，总可以求出对应于电路中任一输出变量的输入—输出方程。在一般情况下，这是一个高阶的常系数线性微分方程。电路越复杂，所含动态元件越多，方程的阶数就越高。
根据前面的分析，可以写出描述单输入—单输出动态电路的输入—输出程的一般形式为
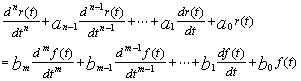（8）
式中r(t)表示电路的输出，f(t)表示作为输人的电压源的电压或电流源的电流的时间函数式。
因此，我们可以说，对单输入—单输出动态电路的分析可以归结为建立以待求变量作为输出变量的输入—输出方程和求解这一方程。
一般地说，如果描述动态电路的输人—输出方程是一阶微分方程，则称该电路为一阶电路。如果输入—输出方程是n阶微分方程，则相应的电路称为n阶电路。据此，图1所示电路为二阶电路，图2所示电路为三阶电路。