动态电路中至少含有一个动态元件，如果动态元件储存了一定数量的能量 ( 电场能量或磁场能量 ) ，即使换路后电路中没有输入激励 ( 独立源 ) ，电路中也会产生电流。这体现了动态元件通过耗能元件进行电磁能量释放的物理过程。电路在无输入激励情况下，仅由动态元件原始储能引起的响应称为零输入响应。零输入响应可以是动态电路中任意支路的电压或电流。
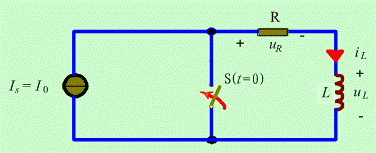
图1 零输入响应实例
如图 1 所示电路，在 
时， 
。在开关闭合后的初瞬，即 
时，有 
，电感元件储存的磁场能量为 
。当开关闭合后， RL 串联电路无激励源作用，电感中的磁场能量将逐步释放直至被电阻 R 消耗完毕为止。在此过程中出现的电感电流 
、电阻电压 
和电感电压 
即为电路的零输入响应。
对一个 n 阶动态电路，如果换路后电路中无输入激励，则其输入 - 输出方程将变为齐次微分方程，具有如下形式：
( 1 )
其中， 
为待求的输出变量。可见，动态电路的零输入响应即齐次微分方程的解。
根据高等数学知识，求解 ( 4-6-1 ) 式 n 阶齐次微分方程，可以先列出其特征方程：
( 2 )
设此特征方程的 n 个特征根分别为 
，且所有的根都互不相等，则 ( 1 ) 式的通解为
( 3 )
这就是 n 阶动态电路零输入响应的一般形式。式中 
是由齐次微分方程式 ( 1 ) 的 n 个初始条件 
决定的积分常数。
由式 ( 3 ) 可以看出，特征根 
决定了动态电路零输入响应的性质。如果特征根都是负实根，则响应随时间的增长而衰减，且特征根的绝对值越大，衰减越快；如果特征根中有复数根，则将出现振荡情况。在物理上，特征根 
取决于电路的拓扑结构及电路中元件参数的取值情况。因此，特征根 
又被称为电路零输入相应的固有频率或自然频率。
【 例1 】 求解例图2 中所给电路的零输入响应 
。 
，
， 
， 
A ， 
V 。
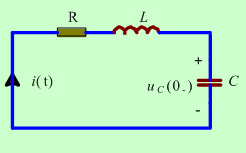
例图2 零输入响应计算实例
解：例图2 中电路在无输入激励情况下的积分微分方程和微分方积分别为
( 4 )
( 5 )
特征方程为
可解得特征根为
， 
该微分方程的通解为
确定常数 
需要初始条件 
、 
。根据题设，易知：
， 
V
在 
时刻，将 
， 
代入 ( 4 ) 式，得
解得： 
A/s
利用两个初始条件，可得
， 
联立求解可得： 
， 
故电路的零输入响应为
