【动态电路】 含有动态元件的电路称为动态电路。
【暂态过程（过渡过程）】由于动态元件的储能特性，动态电路从一个稳态到另一个稳态，中间要经历一个渐变过程，称为过渡过程或暂态过程。
【换路】电路结构的改变、参数的变化、电源的跃变都会引起动态电路的暂态过程。把能引起动态电路暂态过程的因素统称为换路，且认为换路是瞬刻完成的。
动态电路分析即是分析电路在换路后的变化规律。本节将讨论动态电路分析的基本思想与方法。
1、动态电路的微分方程
【输入――输出方程】 动态电路的分析，仍然是根据
、
和电路元件的特性方程，建立关于待求变量与电路输入量之间的关系方程，称之为输入――输出方程。
图6-4-1所示电路，
时换路，要确定
后
的变化规律，则应建立关于与激励的方程。
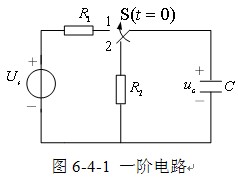
【一阶电路】 由
与
构成的回路的得
这个输入――输出方程为一阶微分方程。电路称为一电路。
【二阶电路】亦可通过，对下图6-4-2所示电路，建立关于
的微分方程。
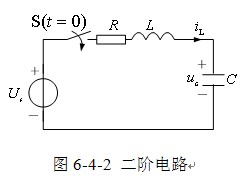
方程为
两边求导得
这是关于
的二阶微分方程。电路称为二阶电路。
【动态电路的阶数】对于线性时不变动态电路，响应与激励的关系为线性常系数微分方程。微分方程的阶数称为电路的阶数。
2、初始条件
【初始条件】若换路发生在时刻，求解微分方程的初始条件是变量及其某些导数在
时刻的值。初始条件不仅与换路后的电路结构、参数、激励情况有关，还与储能元件在换路前已具有的储能有关。
【原始状态】换路前，电路的储能可用
（或
）、
（或
）来表征，独立的、一起称为电路的原始状态。
【初始状态】而
（或
）、
、（或
）表征了电路在时的储能，独立的、一起称为电路的初始状态。
【例6-4-1】 下图（a）所示电路，若
，
，
， 
（DC），
。试确定：
(1) 、、
、
；(2) 
、
、
。
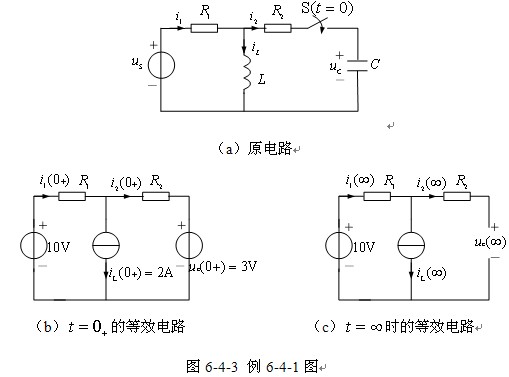
解 (1)确定各变量的值时，必须已知电路的原始状态。
时电路已处于直流激励下的稳态，
相当于短路，相当于开路，
时，该电路的状态连续，即有
值得强调的是，其它变量不具有连续的特点，要确定、。可以利用时刻的
、方程，或用替代定理，得到时刻的等效电路，如图 (b)所示。
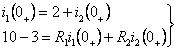
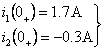
(2) 
后，电路已进入新的稳定状态，对于直流电源作用下的电路，电感相当于短路，电容相当于开路，依此可得到
时的等效电路，如图（c）所示。
3、动态电路的时域分析
通过建立时域的输入输出方程来求解动态电路的方法，称为时域分析法，包括经典的时域分析法和现代的状态变量分析法。经典的时域分析法建立关于输出量与激励的n阶微分方程；状态变量分析法建立关于状态变量和激励的一阶微分方程组。
动态电路分析还可以借助拉普拉斯变换，建立关于输出变量象函数与激励象函数的方程，称为复频域（s域）分析法。